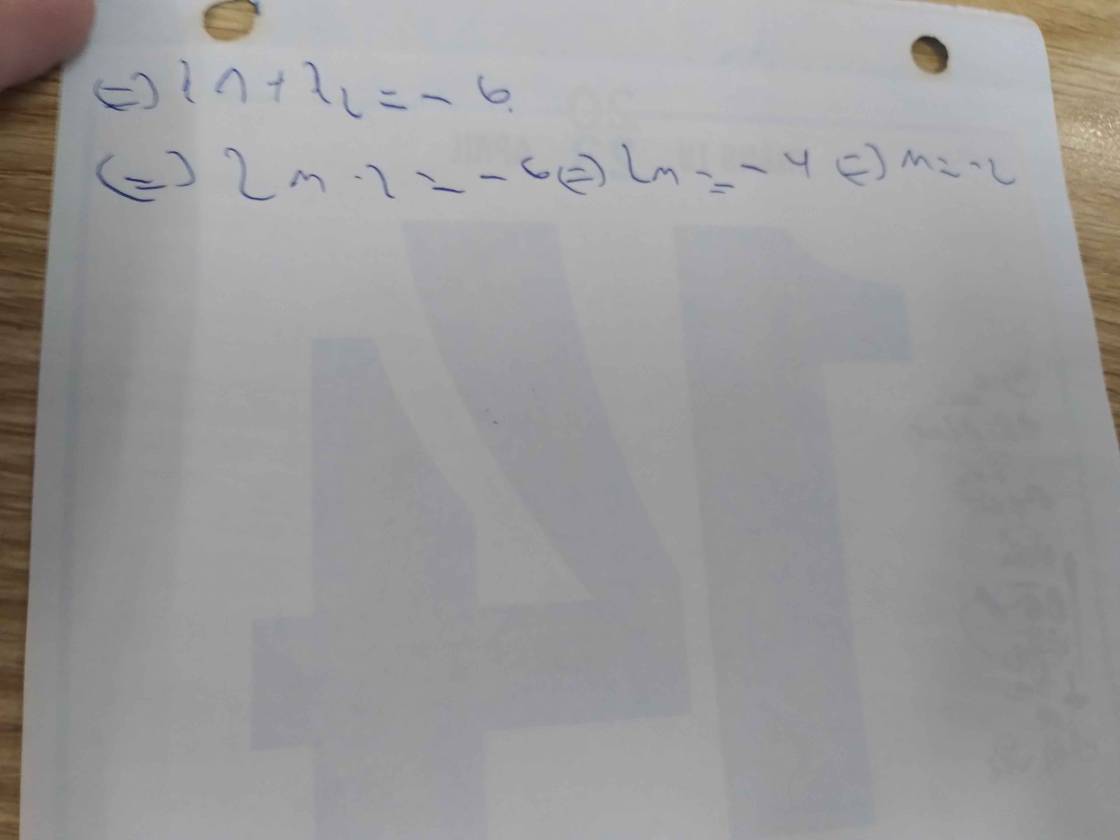Lời giải:

$3^x.x^2=4y(y+1)$ nên $x$ chẵn. Đặt $x=2a$ ta có:

$3^{2a}.a^2=y(y+1)\Leftrightarrow (3^a.a)^2=y(y+1)$

Dễ thấy $(y,y+1)=1$ nên để tích của chúng là scp thì $y,y+1$ là scp.

Đặt $y=m^2; y+1=n^2$ với $m,n$ tự nhiên.

$\Rightarrow 1=(n-m)(n+m)$

$\Rightarrow n=1; m=0\Rightarrow y=0\Rightarrow x=0$

\(a,x^2-6x+5=0\\ \Rightarrow\left(x^2-5x\right)-\left(x-5\right)=0\\ \Rightarrow x\left(x-5\right)-\left(x-5\right)=0\\ \Rightarrow\left(x-1\right)\left(x-5\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)

\(b,2x^2+4x-8=0\\ \Rightarrow x^2+2x-4=0\\ \Rightarrow\left(x^2+2x+1\right)-5=0\\ \Rightarrow\left(x+1\right)^2-\sqrt{5^2}=0\\ \Rightarrow\left(x+1+\sqrt{5}\right)\left(x+1-\sqrt{5}\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=-1-\sqrt{5}\\x=-1+\sqrt{5}\end{matrix}\right.\)

\(c,4y^2-4y+1=0\\ \Rightarrow\left(2y-1\right)^2=0\\ \Rightarrow2y-1=0\\ \Rightarrow y=\dfrac{1}{2}\)

\(d,5x^2-x+2=0\)

Ta có:\(\Delta=\left(-1\right)^2-4.5.2=1-40=-39\)

Vì \(\Delta< 0\Rightarrow\) pt vô nghiệm

\(\Delta=m^2-4\left(m-4\right)=\left(m^2-4m+4\right)+12=\left(m-2\right)^2+12>0;\forall m\)

Suy ra pt luôn có hai nghiệm pb với mọi m

Theo viet có:\(\left\{{}\begin{matrix}x_1+x_2=m\\x_1.x_2=m-4\end{matrix}\right.\)

\(\left(5x_1-1\right)\left(5x_2-1\right)< 0\)

\(\Leftrightarrow25x_1x_2-5\left(x_1+x_2\right)+1< 0\)

\(\Leftrightarrow25\left(m-4\right)-5m+1< 0\)

\(\Leftrightarrow m< \dfrac{99}{20}\)

Vậy...

\(\Delta=m^2-4m+16=\left(m-2\right)^2+12>0\)

\(\Rightarrow\) pt luôn có 2 nghiệm phân biệt

Áp dụng hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-4\end{matrix}\right.\)

Ta có: \(\left(5x_1-1\right)\left(5x_2-1\right)=25x_1x_2-5\left(x_1+x_2\right)+1\)

\(=25\left(m-4\right)-5m+1=20m-99\)

\(\Rightarrow20m-99< 0\Rightarrow m< \dfrac{99}{20}\)

Lời giải:
$x^2-2y^2=5\Rightarrow x$ lẻ. Đặt $x=2k+1$ với $k$ nguyên 

$x^2-2y^2=5$

$\Leftrightarrow (2k+1)^2-2y^2=5$

$\Leftrightarrow 2k^2+2k-y^2=2$

$\Rightarrow y$ chẵn. Đặt $y=2t$ với $t$ nguyên

PT trở thành: $2k^2+2k-4t^2=2$
$\Leftrightarrow k^2+k-2t^2=1$

Điều này vô lý do $k^2+k-2t^2=k(k+1)-2t^2$ chẵn còn $1$ thì lẻ

Vậy pt vô nghiệm.

Lời giải:

$x^2+4y^2-2xy=13$
$\Leftrightarrow (x^2+y^2-2xy)+3y^2=13$

$\Leftrightarrow (x-y)^2+3y^2=13$

$\Rightarrow 3y^2=13-(x-y)^2\leq 13< 15$

$\Rightarrow y^2< 5$

Vì $y^2\geq 0$ với mọi $y$ nguyên nên $y^2\in\left\{0; 1;4\right\}$

Với $y^2=0$:

$(x-y)^2=13-3y^2=13$ (loại vì 13 không là scp)

Với $y^2=1$:

$(x-y)^2=13-3y^2=10$ (loại vì 10 không là scp)

Với $y^2=4$:

$(x-y)^2=13-3y^2=1$

$\Rightarrow x-y=\pm 1$

$\Rightarrow x=y\pm 1$

$y^2=4\Rightarrow y=\pm 2$

Với $y=2$ thì $x=1$ hoặc $x=3$

Với $y=-2$ thì $x=-3$ hoặc $y=-1$

b: \(\text{Δ}=\left(2m+3\right)^2-4\left(4m+2\right)\)

\(=4m^2+12m+9-16m-8\)

\(=4m^2-4m+1=\left(2m-1\right)^2>=0\)

Do đó: Phương trình luôn có hai nghiệm

Theo đề, ta có:

\(\left\{{}\begin{matrix}2x_1-5x_2=6\\x_1+x_2=2m+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1-5x_2=6\\2x_1+2x_2=4m+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-7x_2=-4m\\2x_1=5x_2+6\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{4}{7}m\\2x_1=\dfrac{20}{7}m+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{4}{7}m\\x_1=\dfrac{10}{7}m+3\end{matrix}\right.\)

Theo đề, ta có: \(x_1x_2=4m+2\)

\(\Rightarrow4m+2=\dfrac{40}{49}m^2+\dfrac{12}{7}m\)

\(\Leftrightarrow m^2\cdot\dfrac{40}{49}-\dfrac{16}{7}m-2=0\)

\(\Leftrightarrow40m^2-112m-98=0\)

\(\Leftrightarrow40m^2-140m+28m-98=0\)

=>\(20m\left(2m-7\right)+14\left(2m-7\right)=0\)

=>(2m-7)(20m+14)=0

=>m=7/2 hoặc m=-7/10

Hai phương trình không tương đương.

ai đó giải hộ được không ạ  ' _ '

\(x^3-5x^2+2mx+5x-4m+2=0\)

\(\Leftrightarrow\left(x^3-5x^2+5x+2\right)+2m\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x^2-3x-1\right)+2m\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x^2-3x+2m-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x^2-3x+2m-1=0\left(1\right)\end{matrix}\right.\)

a. Pt đã cho có 3 nghiệm pb khi và chỉ khi (1) có 2 nghiệm pb khác 2

\(\Leftrightarrow\left\{{}\begin{matrix}4-6+2m-1\ne0\\\Delta=9-4\left(2m-1\right)>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{3}{2}\\m< \dfrac{13}{8}\end{matrix}\right.\)

b. Do vai trò 3 nghiệm như nhau, không mất tính tổng quát, giả sử \(x_1;x_2\) là nghiệm của (1) và \(x_3=2\)

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=2m-1\end{matrix}\right.\)

\(x_1^2+x_2^2+x_3^2=11\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+4=11\)

\(\Leftrightarrow9-2\left(2m-1\right)-7=0\)

\(\Leftrightarrow m=1\)