Tìm khoảng đồng biến và nghịch biến của hàm số y = \(\dfrac{x+3}{2x-5}\)

Những câu hỏi liên quan
tìm khoảng đồng biến nghịch biến của hàm số sau
a) y = \(\dfrac{x-1}{x+1}\)
b) y = \(\dfrac{2x+1}{8x-1}\)
a: \(y'=\dfrac{\left(x-1\right)'\left(x+1\right)-\left(x-1\right)\left(x+1\right)'}{\left(x+1\right)^2}\)
\(=\dfrac{x+1-x+1}{\left(x+1\right)^2}=\dfrac{2}{\left(x+1\right)^2}>0\)
=>Hàm số luôn đồng biến khi x<>-1
vậy: Các khoảng đồng biến là \(\left(-\infty;-1\right);\left(-1;+\infty\right)\)
b: \(y'=\dfrac{\left(2x+1\right)'\left(8x-1\right)-\left(2x+1\right)\left(8x-1\right)'}{\left(8x-1\right)^2}\)
\(=\dfrac{2\left(8x-1\right)-8\left(2x+1\right)}{\left(8x-1\right)^2}\)
\(=\dfrac{16x-2-16x-8}{\left(8x-1\right)^2}=-\dfrac{10}{\left(8x-1\right)^2}< 0\)
=>Hàm số nghịch biến khi x<>1/8
Vậy: Các khoảng nghịch biến là \(\left(-\infty;\dfrac{1}{8}\right);\left(\dfrac{1}{8};+\infty\right)\)
Đúng 0
Bình luận (0)
Cho hàm số: \(y=\dfrac{x^2-2x-1}{x-1}\) Tìm khoảng đồng biến và nghịch biến của hàm số đã cho:
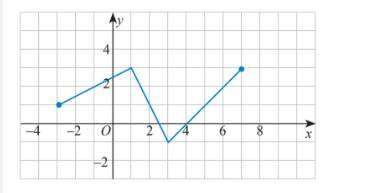
a) Tìm khoảng đồng biến và nghịch biến của hàm số có đồ thị sau:
b) Xét tính đồng biến, nghịch biến của hàm số \(y = f(x) = 5{x^2}\) trên khoảng (2; 5).
a) Từ đồ thị ta thấy hàm số xác định trên [-3;7]
+) Trên khoảng (-3; 1): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (-3; 1).
+) Trên khoảng (1; 3): đồ thị có dạng đi xuống từ trái sang phải nên hàm số này nghịch biến trên khoảng (1; 3).
+) Trên khoảng (3; 7): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (3; 7).
b) Xét hàm số \(y = 5{x^2}\) trên khoảng (2; 5).
Lấy \({x_1},{x_2} \in (2;5)\) là hai số tùy ý sao cho \({x_1} < {x_2}\).
Do \({x_1},{x_2} \in (2;5)\) và \({x_1} < {x_2}\) nên \(0 < {x_1} < {x_2}\), suy ra \({x_1}^2 < {x_2}^2\) hay \(5{x_1}^2 < 5{x_2}^2\)
Từ đây suy ra \(f({x_1}) < f({x_2})\)
Vậy hàm số đồng biến (tăng) trên khoảng (2; 5).
Đúng 0
Bình luận (1)
tìm khoảng đồng biến và nghịch biến của hàm số sau
a) y' = \(\left(2x-3\right)\left(x^2-1\right)\)
b) y' = \(-\left(x+2\right)\left(2x+5\right)\)
a: Đặt y'>0
=>(2x-3)(x^2-1)>0
Th1: 2x-3>0 và x^2-1>0
=>x>3/2 và (x>1 hoặc x<-1)
=>x>3/2
TH2: 2x-3<0 và x^2-1<0
=>x<3/2 và -1<x<1
=>-1<x<1
=>Hàm số đồng biến khi x>3/2 hoặc -1<x<1
Đặt y'<0
=>(2x-3)(x^2-1)<0
TH1: 2x-3>0 và x^2-1<0
=>x>3/2 và -1<x<1
=>Loại
TH2: 2x-3<0 và x^2-1>0
=>x<3/2 và (x>1 hoặc x<-1)
=>1<x<3/2 hoặc x<-1
=>Hàm số nghịch biến khi 1<x<3/2 hoặc x<-1
b: Đặt y'>0
=>(x+2)(2x+5)<0
=>-5/2<x<-2
=>hàm số đồng biến khi -5/2<x<-2
Đặt y'<0
=>(x+2)(2x+5)>0
=>x>-2 hoặc x<-5/2
=>Hàm số nghịch biến khi x>-2 hoặc x<-5/2
Đúng 0
Bình luận (0)
tìm các giá trị của m để hàm số
a) \(y=\dfrac{x+m}{x+1}\) nghịch biến trên từng khoảng xác định
b) \(y=\dfrac{2x-3m}{x-m}\) đồng biến trên từng khoảng xác định
a: TXĐ: D=R\{-1}
\(y'=\dfrac{\left(x+m\right)'\left(x+1\right)-\left(x+1\right)'\left(x+m\right)}{\left(x+1\right)^2}\)
\(=\dfrac{x+1-x-m}{\left(x+1\right)^2}=\dfrac{1-m}{\left(x+1\right)^2}\)
Để hàm số nghịch biến trên từng khoảng xác định thì \(y'< 0\forall x\)
=>\(\dfrac{1-m}{\left(x+1\right)^2}< 0\)
=>1-m<0
=>m>1
b: TXĐ: D=R\{m}
\(y=\dfrac{2x-3m}{x-m}\)
=>\(y'=\dfrac{\left(2x-3m\right)'\left(x-m\right)-\left(2x-3m\right)\left(x-m\right)'}{\left(x-m\right)^2}\)
\(=\dfrac{2\left(x-m\right)-\left(2x-3m\right)}{\left(x-m\right)^2}=\dfrac{2x-2m-2x+3m}{\left(x-m\right)^2}\)
\(=\dfrac{m}{\left(x-m\right)^2}\)
Để hàm số đồng biến trên từng khoảng xác định thì \(y'>0\forall x\)
=>\(\dfrac{m}{\left(x-m\right)^2}>0\)
=>m>0
Đúng 0
Bình luận (0)
1) tìm khoảng đồng biến nghịch biến \(y=\dfrac{x^2-6x+10}{x-3}\)
2) hàm số \(y=\dfrac{mx-4}{x-m}\) đồng biến trên khoảng (0,\(+\infty\))
1: TXĐ: D=R\{3}
\(y=\dfrac{x^2-6x+10}{x-3}\)
=>\(y'=\dfrac{\left(x^2-6x+10\right)'\left(x-3\right)-\left(x^2-6x+10\right)\left(x-3\right)'}{\left(x-3\right)^2}\)
=>\(y'=\dfrac{\left(2x-6\right)\left(x-3\right)-\left(x^2-6x+10\right)}{\left(x-3\right)^2}\)
=>\(y'=\dfrac{2x^2-12x+18-x^2+6x-10}{\left(x-3\right)^2}\)
=>\(y'=\dfrac{x^2-6x+8}{\left(x-3\right)^2}\)
Đặt y'<=0
=>\(\dfrac{x^2-6x+8}{\left(x-3\right)^2}< =0\)
=>\(x^2-6x+8< =0\)
=>(x-2)(x-4)<=0
=>2<=x<=4
Vậy: Khoảng đồng biến là [2;3) và (3;4]
Đúng 1
Bình luận (0)
tìm khoảng đồng biến và nghịch biến của hàm số y = g(x) = f(2x-4)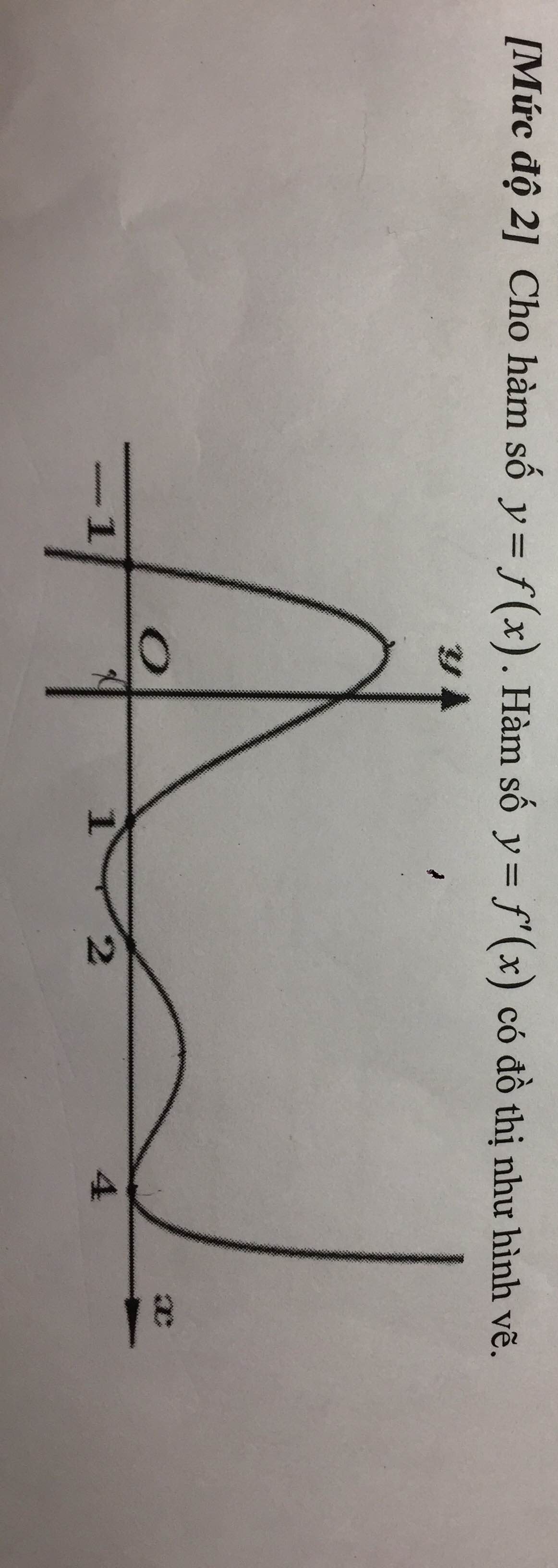
Cho hàm số yf(x) xác định trên
ℝ
và có đồ thị của hàm số f’(x) và các khẳng định sau:(1). Hàm số yf(x) đồng biến trên khoảng
1
;
+
∞
(2). Hàm số yf(x) nghịch biến trên khoảng
-
∞
;
-
2
(3). Hàm số yf(x) nghịch biến trên khoảng
-...
Đọc tiếp
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f’(x) và các khẳng định sau:
(1). Hàm số y=f(x) đồng biến trên khoảng 1 ; + ∞
(2). Hàm số y=f(x) nghịch biến trên khoảng - ∞ ; - 2
(3). Hàm số y=f(x) nghịch biến trên khoảng - 2 ; 1 .
(4). Hàm số y = f x 2 đồng biến trên khoảng - 1 ; 0
(5). Hàm số y = f x 2 nghịch biến trên khoảng (1;2)

Số khẳng định đúng là
A. 4
B. 3
C. 2
D. 5
Phát biểu các điều kiện để hàm số đồng biến, nghịch biến. Tìm các khoảng đơn điệu của các hàm số:
\(y= -x^3 + 2x^2 – x – 7\)
\(y=\dfrac{x-5}{1-x}\)
*Xét hàm số: y= -x3 + 2x2 – x – 7
Tập xác định: D = R
\(y'\left(x\right)=-3x^2+4x-1\); \(y'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{3}\end{matrix}\right.\)
y’ > 0 với và y’ < 0 với \(x \in ( - \infty ,{1 \over 3}) \cup (1, + \infty )
Vậy hàm số đồng biến trong (\(\dfrac{1}{3}\),1)(\(\dfrac{1}{3}\),1) và nghịch biến trong (−∞,13)∪(1,+∞)(−∞,13)b) Xét hàm số: \(y=\dfrac{x-5}{1-x}\).
Tập xác định: D = R{1}
\(y'=\dfrac{-4}{\left(1-x\right)^2}< 0,\forall x\in D\)
Vậy hàm số nghịch biến trong từng khoảng (-∞,1) và (1, +∞)
Đúng 1
Bình luận (0)















