Cho các góc lượng giác a, b thỏa mãn cos 2 a + cos 2 b = m m ∈ ℝ . Giá trị của biểu thức P = cos a + b . cos a - b là
A. P = m 2 - 1
B. P = 1 - m 2
C. P = m - 1
D. P = m + 1
Cho tam giác ABC không tù, thỏa mãn điều kiện \(\cos2A+2\sqrt{2}\cos B+2\sqrt{2}\cos C=3\)
Tính các góc của tam giác ABC ?
Có: cos 2A + 2√2.cos B + 2√2.cos C = 3
⇔2cos²A - 1 + 2√2.2.cos[(B + C)/2] . cos[(B - C)/2] - 3 = 0
⇔2cos²A + 4√2.sin (A/2) . cos[(B - C)/2] - 4 = 0(1)
Ta thấy: sin(A/2) > 0 ; cos[(B - C)/2] ≤ 1
⇒VT ≤ 2cos²A + 4√2.sin(A/2) - 4
Vì tam giác ABC không tù nên 0 ≤ cos A < 1
⇒cos²A ≤ cos A
⇒VT ≤ 2cos A + 4√2.sin(A/2) - 4
⇒VT ≤ 2.[1 - 2.(sin A/2)²] + 4√2.sin(A/2) - 4
⇒VT ≤ -4.(sin A/2)² + 4√2.sin(A/2) - 2
⇒VT ≤ -2(√2.sin A/2 - 1)² ≤ 0(2)
Kết hợp (1)(2) thì đẳng thức xảy ra khi tất cả các dấu = ở trên xảy ra
⇔cos [(B - C)/2] = 1 và cos²A = cos A và √2.sin A/2 - 1 = 0
⇔góc B = góc C và cos A = 0 và sin A/2 = 1/√2
⇔ góc B = góc C và góc A = 90 độ
Vậy góc A = 90 độ, góc B = góc C = 45 độ
Cho tam giác ABC thỏa mãn hệ thức b + c = 2a. Trong các mệnh đề sau, mệnh đề nào đúng?
A. CosB + Cos C = 2 Cos A B. Sin B + Sin C = 2 Sin A
C. Sin B + Sin C = \(\dfrac{1}{2}SinA\) D. Sin B + Sin C = 2 Sin A
Theo đl sin có:
\(\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}\Rightarrow b=a\dfrac{sinB}{sinA};c=\dfrac{sinC}{sinA}.a\)
Mà `b+c=2a`
\(\Rightarrow a\dfrac{sinB}{sinA}+a\dfrac{sinC}{sinA}=2a\\ \Rightarrow\dfrac{sinB}{sinA}+\dfrac{sinC}{sinA}=2\\ \Leftrightarrow sinB+sinC=2sinA\)
Chọn B
Cho a,b,c la số đo của các góc nhọn thỏa mãn cos2 a + cos2 b+ cos2 c \(\ge\)2. CMR (tan a*tan b* tan c)2 \(\le\)1/8
Cho hai góc nhọn a và b thỏa mãn cosa = 1/3, cos b = 1/4.Giá trị của cos( a + b) cos (a - b) bằng :
![]()
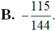
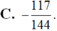
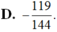
Chọn D.
Áp dụng công thức biến đổi tích thành tổng và công thức nhân đôi ta có:
cos( a + b) cos (a - b)= ½ . ( cos 2a + cos2b)
= cos2a + cos2b - 1 = 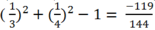
2) Cho △ABC thỏa mãn hệ thức \(b+c=2a\). Mệnh đề nào trong các mệnh đề sau đúng?
\(A.\cos B+\cos C=2\cos A\)
\(B.\sin B+\sin C=2\sin A\)
\(C.\sin B+C=\dfrac{1}{2}\sin A\)
\(D.\sin B+\cos C=2\sin A\)
BÀI 1 :cho tam giác ABC vuông tại A có AB=4cm BC=6cm. tính tỉ số lượng giác của các góc B và C
BÀI 2 :đơn giản các biểu thức
a)\(A=\cos^2x+\cos^2x.\cot g^2x\)
b)\(sin^2x+\sin^2x.\tan^2x\)
c)\(\dfrac{2cos^2x-1}{\sin x+\cos x}\)
d)\(\dfrac{\cos x}{1+\sin x}+\tan x\)
Cho A,B,C là các góc của tam giác. Chứng minh các đẳng thức sau: a. cos(A+B)+cosC=0 b. cosA+B/2=sinC/2 c. cos(A-B)+cos(2B+C)=0
a) \(cos\left(A+B\right)+cosC=0\)
\(\Leftrightarrow cos\left(\pi-C\right)+cosC=0\)
\(\Leftrightarrow-cosC+cosC=0\)
\(\Leftrightarrow0=0\left(đúng\right)\)
\(\Leftrightarrow dpcm\)
b) \(cos\left(\dfrac{A+B}{2}\right)=sin\dfrac{C}{2}\)
\(\Leftrightarrow cos\left(\dfrac{\pi-C}{2}\right)=sin\dfrac{C}{2}\)
\(\Leftrightarrow cos\left(\dfrac{\pi}{2}-\dfrac{C}{2}\right)=sin\dfrac{C}{2}\)
\(\Leftrightarrow sin\dfrac{C}{2}=sin\dfrac{C}{2}\left(đúng\right)\)
\(\Leftrightarrow dpcm\)
c) \(cos\left(A-B\right)+cos\left(2B+C\right)=0\left(1\right)\)
Ta có : \(A+B+C=\pi\)
\(\Leftrightarrow2B+C=\pi-A+B\)
\(\Leftrightarrow2B+C=\pi-\left(A-B\right)\)
\(\left(1\right)\Leftrightarrow cos\left(A-B\right)+cos\left[\pi-\left(A-B\right)\right]=0\)
\(\Leftrightarrow cos\left(A-B\right)-cos\left(A-B\right)=0\)
\(\Leftrightarrow0=0\left(đúng\right)\)
\(\Leftrightarrow dpcm\)
Cho tam giác ABC có A là góc tù. Xét dấu các biểu thức.
a, M = sin a + sin b + sin c.
b, M = sos a . cos b . cos c
c, D = cos a/2 . sin b/2 . cot c/2
d, D = cot a . tan b . cot c
Mong mọi người giúp đỡ ạ!
a) Giải phương trình \(\cos x = - \frac{1}{2}\)
b) Tìm góc lượng giác x sao cho \(\cos x = \cos \left( { - {{87}^ \circ }} \right)\)
a) \(\cos x = - \frac{1}{2} \Leftrightarrow \cos x = \cos \left( {\frac{{2\pi }}{3}} \right) \Leftrightarrow \left[ \begin{array}{l}x = \frac{{2\pi }}{3} + k2\pi \\x = - \frac{{2\pi }}{3} + k2\pi \end{array} \right.\)
b) \(\cos x = \cos \left( { - {{87}^ \circ }} \right) \Leftrightarrow \left[ \begin{array}{l}x = - {87^ \circ } + k.360\\x = {87^ \circ } + k{.360^ \circ }\end{array} \right.\)
Cho ΔABC thỏa mãn: \(cos\dfrac{C}{2}.cos\left(A-B\right)+cosC.cos\left(\dfrac{A-B}{2}\right)=0\)
Tính \(sinA+sinB\)