Chứng minh D Ax ^ = B C N ^ theo nhiều cách
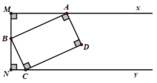
Cho đoạn thẳng AB có M là trung điểm. Trên hai nửa mặt phẳng đối nhau bờ là đường thẳng AB, kẻ các tia Ax và By song song với nhau. Trên Ax lấy điểm C, trên By lấy điểm D sao cho AC = BD. Kẻ AH MC (H CM) ; kẻ BK MD (K MD).
a. Chứng minh rằng: ∆ACM = ∆BDM
b. Chứng minh rằng: AH = BK
c. Chứng minh C, M, D thẳng hàng.
Giải theo cách lp7
Cho △ABC có ∠A=120 độ,kẻ phân giác Ax của ∠A.Trên tia Ax lấy điểm E sao cho AE=AB+AC.Trên tia Ax lấy điểm D sao cho AD=AB
a,Chứng minh △ABD đều
b,Chứng minh △ABC=△DBE
c,Chứng minh △BCE đều
Giảng bài: cho đường tròn tâmO bán kính R đường kính AB kẻ tiếp tuyến AX tại A lấy M thuộc AX kẻ tiếp tuyến MC tới đường tròn C là tiếp điểm gọi H là trực tâm của tam giác MAC a, chứng minh: MCBO là hình thang b, cho góc ABC bằng 60 độ tính theo R độ dài đoạn thẳng MA c, chứng minh: khi M chuyển động trên AX thì H thuộc một đường tròn cố định
Cho tam giác ABC vuông tại A. Tia Ax đi qua trung điểm M của BC. Kẻ BE và CF cùng vuông góc với Ax ( E thuộc Ax, F thuộc Ax). Chứng minh:
a)Chứng minh tam giác AOM =tam giác BOM
b) chứng minh AM = BM
c) qua H thuộc tia Ot, kẻ đường cuông góc với Ot, nó cắt Ox và Oy theo thứ tự tại C và D
Chứng minh AB song song CD
Cho nửa đường tròn (O) đường kính AB. Vẽ 2 tiếp tuyến Ax; By (Ax; By cùng nằm trên nửa mặt phẳng bờ AB). Qua M bất kỳ trên (O) (M khác A,B) kẻ tiếp tuyến thứ 3 cắt Ax, By theo thứ tự C,D. Gọi N là giao điểm của AD và BC.
a) Chứng minh A,C,M,O cùng thuộc một đường tròn
b) Chứng minh AC. BD không đổi khi M di chuyển trên (O)
c) Chứng minh MN ⊥ AB
d) Chứng minh MN= OC^2.OD^2/ CD^3
giúp mk vs! mk đang cần gấp
Gợi ý:
a) Có \(A,M\) cùng nhìn \(CO\) dưới góc \(90^o\) nên \(A,C,M,O\) cùng thuộc một đường tròn.
b) \(CA=CM,DB=DM\) (tính chất hai tiếp tuyến cắt nhau)
Xét tam giác \(COD\) vuông tại \(O\) đường cao \(OM\):
\(OM^2=CM.DM=AC.BD\).
c) Kẻ \(MH\perp AB\). Kéo dài \(BM\) cắt \(Ax\) tại \(E\).
Tam giác \(AME\) vuông tại \(M\) có \(CM=CA\) do đó \(C\) là trung điểm của \(AE\).
Suy ra \(BC\) đi qua trung điểm của \(MH\).
Tương tự ta cũng chứng minh được \(AD\) đi qua trung điểm của \(MH\).
Vậy \(M,N,H\) thẳng hàng suy ra \(MN\perp AB\).
d) Ta có \(\dfrac{OC^2.OD^2}{CD^3}=\dfrac{\left(OC.OD\right)^2}{CD^3}=\dfrac{\left(OM.CD\right)^2}{CD^3}=\dfrac{OM^2}{CD}\).
\(\dfrac{DM}{DC}=\dfrac{MN}{AC},\dfrac{CM}{DC}=\dfrac{MN}{BD}\) suy ra \(\dfrac{DM+CM}{DC}=MN\left(\dfrac{1}{AC}+\dfrac{1}{BD}\right)\)
\(\Leftrightarrow MN=\dfrac{AC.BD}{AC+BD}=\dfrac{OM^2}{CD}\).
Suy ra đpcm.
Cho đường tròn (O;R) có đường kính AB. Vẽ tiếp tuyến Ax, lấy M bất kì thuộc tia Ax, MB cắt đường tròn (O) tại C.
a) chứng minh AC vuông góc với MB.
b) tính BC.BM theo R.
c) vẽ dây AD vuông góc với OM tại H. Chứng minh MD2 = MC.MB.
............giúp mk vs.............
Đây nhé
a, Ta có Xét tam giác ABC có:
OC là trung tuyến của tam giác ABC
OC=OA=OB
Suy ra tam giác ABC vuông tại C
Vậy AC vuông góc với MB
b,Xét tam giác AMB vuông tại A có AC là đường cao
suy ta BC.BM=AB^2=4R^2(hệ thức lượng tam giác vuông )
c,Ta có:
TAm giác ADO cân tại O có OH là đường cao
suy ra H:trung điểm AD
suy ra tam giác AMD cân tại M
suy ra AM=MD
Tam giác AMB vuông tại A có đường cao AC
suy ra AM^2=MC.MB(hệ thức luợng tam giác vuông)
Suy ra MD^2=MC.MB
Nhận xét: Câu c là phương tích trong đường tròn
bạn học hệ thức lượng trong đường tròn chưa
Giúp mình với
Cho 1/2 đường tròn(O) đường kính AB=2R. Kẻ các tiếp tuyến Ax,By cùng phía với nửa đường tròn (O) đường kính AB. Vẽ bán kính OE bất kì. Tiếp tuyến với đường tròn tâm O tại E cắt Ax,By theo tứ tự ở C và D.
a) chứng minh CD=AB+BD
b) Tính góc COR
c) Chứng minh AC.BD= R2
Tính diện tích ABCD theo R biết AC=R/2.
d) chứng minh AB là tiếp tuyến của đường tròn đường kính CD.
a: Xét (O) có
CA,CE là các tiếp tuyến
nên CA=CE và OC là phân giác của góc AOE(1)
Xét (O) có
DE,DB là các tiếp tuyến
nên DE=DB và OD là phân giác của góc EOB(2)
Ta có: CE+ED=CD
nên CD=CA+DB
b: Từ (1) và (2) suy ra \(\widehat{COD}=\dfrac{1}{2}\left(\widehat{EOA}+\widehat{EOB}\right)=\dfrac{1}{2}\cdot180^0=90^0\)
c: \(AC\cdot BD=CE\cdot ED=OE^2=R^2\)
d: Gọi M là trung điểm của CD
Xét tứ giác ACDB có
O,M lần lượt là trung điểm của AB và CD
nên OM là đường trung bình
=>OM//AC//BD
hay OM vuông góc với AB
Vì ΔCOD vuông tại O
mà M là trung điểm của CD
nên M là tâm đường tròn ngoại tiếp ΔCOD
=>AB là tiếp tuyến tại O của (M)
Cho nửa đường tròn tâm O , đường kính AB = 2R . M là 1 điểm tùy ý trên đường tròn, M khác A, B. Kẻ 2 tiêp stuyeens Ax, By với nửa đường trong ( Ax, By và nửa đường trong cùng nằm trên một mặt phẳng bờ AB ) . Qua M kẻ tiếp tuyến thứ 3 với đường trong cắt Ax và By tại C và D .
a). Chứng minh : CD = AC + BD và tam giác COD vuông tại O
b). Chứng minh : AC.BD = R2
c). Cho biết AM = R . Tính theo R diện tích tam giác BDM
d). AD cắt BC tại N. Chứng minh MN song song AC
a: Xét (O) có
CA là tiếp tuyến
CM là tiếp tuyến
Do đó: CA=CM và OC là phân giác của góc MOA(1)
Xét(O) có
DM là tiếp tuyến
DB là tiếp tuyến
Do đó: DM=DB và OD là phân giác của góc MOB(2)
Ta có: CD=CM+MD
nên CD=CA+DB
Từ (1) và (2) suy ra góc COD=1/2góc AOB=90 độ
b: Xét ΔOCD vuông tại O có OMlà đường cao
nên \(OM^2=CM\cdot MD\)
=>\(R^2=AC\cdot BD\)
c: Xét ΔOAM có OA=OM=AM
nên ΔOAM đều
=>góc MOA=60 độ
=>góc MDB=60 độ
\(MB=R\sqrt{3}\)
\(S_{BDM}=\dfrac{MB^2\cdot\sqrt{3}}{4}=\dfrac{R^2\cdot3\cdot\sqrt{3}}{4}\)
Trên một đường thẳng (d) cho hai điểm A, B. Các đường thẳng tia Ax, By cùng nằm trong nửa mặt phẳng bờ là đường thẳng (d). Trên Ax lấy 1 điểm C, trên By lấy 1 điểm D thỏa AB2 = 4AC.BD. Vẽ các đường tròn tâm C và D và theo thứ tự, tiếp xúc với (d) tại các điểm A,B. Chứng minh : hai đường tròn đó tiếp xúc với nhau.
Trên một đường thẳng (d) cho hai điểm A, B. Các đường thẳng tia Ax, By cùng nằm trong nửa mặt phẳng bờ là đường thẳng (d). Trên Ax lấy 1 điểm C, trên By lấy 1 điểm D thỏa AB2 = 4AC.BD. Vẽ các đường tròn tâm C và D và theo thứ tự, tiếp xúc với (d) tại các điểm A,B. Chứng minh : hai đường tròn đó tiếp xúc với nhau.