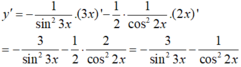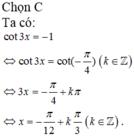cot3x=tan2x

Những câu hỏi liên quan
Hàm số
y
c
o
t
3
x
-
1
2
tan
2
x
có đạo hàm là: A.
-
3
s
i
n
2
3
x
+
1
c
o
s
2...
Đọc tiếp
Hàm số y = c o t 3 x - 1 2 tan 2 x có đạo hàm là:
A. - 3 s i n 2 3 x + 1 c o s 2 2 x
B. - 3 s i n 2 3 x - 1 c o s 2 2 x
C. - 3 s i n 2 3 x - x c o s 2 2 x
D. - 1 s i n 2 3 x - 1 c o s 2 2 x
Cho bốn hàm số:
1
y
sin
2
x
;
2
y
cos
4
x
;
3
y
tan
2
x
;
4
y
cot
3
x
Có mấy hàm số tuần hoàn với chu kì
π
2
?
A. 0 B. 2 C. 3 D. 1
Đọc tiếp
Cho bốn hàm số:
1
y
=
sin
2
x
;
2
y
=
cos
4
x
;
3
y
=
tan
2
x
;
4
y
=
cot
3
x
Có mấy hàm số tuần hoàn với chu kì
π
2
?
A. 0
B. 2
C. 3
D. 1
Tính giá trị của biểu thức:
a) tan10o . tan11o ... tan79o . tan80o
b) Cho tan x+ cot x=2. tính tan2x + cot2x ; tan3x + cot3x
\(a,\tan10.\tan11......\)
\(=\left(\tan10.tan80\right)\left(tan11.tan79\right)....\left(tan44.tan46\right).tan45\)
Mà 10 và 80, 11 và 79, ... là các góc phụ nhau .
\(=tan10.cot10....tan45=1\)
b, Ta có : \(\tan x+\cot x=2\)
\(\Rightarrow\tan^2x+2\tan x\cot x+\cot^2x=4\)
\(\Rightarrow\tan^2x+\cot^2x=4-2=2\)
Ta có : \(\tan^3x+\cot^3x=\left(\tan x+\cot x\right)\left(\tan^2x-\tan x\cot x+\cot^2x\right)=2\)
Đúng 0
Bình luận (0)
Trong bốn hàm sô: y=sin2x; y=cos4x; y=tan2x; y=cot3x có mấy hàm số tuần hoàn với chu kì pi/2
tìm tập xác định của hàm số
1.y=\(cot\left(\dfrac{\pi}{3}-x\right)\)
2.y=\(\dfrac{tan2x-1}{\sqrt{1+sinx}+1}\)
3.y=\(\sqrt{\sqrt{1+sinx}-\sqrt{2}}\)
4.y=\(\dfrac{3cos4x-3}{\sqrt{2-2cosx}-2}\)
5.y=\(\dfrac{1-cot3x}{1-\sqrt{1+sin3x}}\)
6.y=\(cot2x+cotx\)
1. \(sin\left(\dfrac{\pi}{3}-x\right)\ne0\Leftrightarrow\dfrac{\pi}{3}-x\ne k\pi\Leftrightarrow x\ne\dfrac{\pi}{3}-k\pi\)
2. \(cos2x\ne0\Leftrightarrow2x\ne\dfrac{\pi}{2}+k\pi\Leftrightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
3. \(\sqrt{1+sinx}-\sqrt{2}\ge0\Leftrightarrow1+sinx\ge2\Leftrightarrow sinx\ge1\Leftrightarrow sinx=1\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)
4. \(\sqrt{2-2cosx}-2\ne0\Leftrightarrow2-2cosx\ne4\Leftrightarrow cosx\ne-1\Leftrightarrow x\ne\pi+k2\pi\)
5. \(1-\sqrt{1+sin3x}\ne0\Leftrightarrow sin3x\ne0\Leftrightarrow3x\ne k\pi\Leftrightarrow x\ne\dfrac{k\pi}{3}\)
Đúng 1
Bình luận (2)
Giải các phương trình :
a) \(\cos3x-\sin2x=0\)
b) \(\tan x\tan2x=-1\)
c) \(\sin3x+\sin5x=0\)
d) \(\cot2x\cot3x=1\)
Tìm tập xác định của hàm số sau :
1) \(y=\frac{tan2x-1}{\sqrt{1+sinx}+1}\)
2)\(y=\frac{3cos4x-3}{\sqrt{2-2cosx}-2}\)
3)\(y=\frac{1-cot3x}{1-\sqrt{1+sin3x}}\)
1/ ĐKXĐ: \(cos2x\ne0\Rightarrow2x\ne k\frac{\pi}{2}\Rightarrow x\ne\frac{k\pi}{4}\)
2/ ĐKXĐ:
\(\sqrt{2-2cosx}\ne2\Rightarrow2-2cosx\ne4\)
\(\Rightarrow cosx\ne-1\Rightarrow x\ne\pi+k2\pi\)
3/ ĐKXĐ: \(sin3x\ne0\Rightarrow3x\ne k\pi\Rightarrow x\ne\frac{k\pi}{3}\)
Đúng 0
Bình luận (6)
chứng minh
a> cot2x/1+cot2x . 1+tan2x/tan2x = tan2x+cot2x/1=tan4x
b>tan2x-cos2x/sin2x + cot2x-sin2x/cos2x = 2
a: \(VT=\dfrac{cot^2x}{1+cot^2x}\cdot\dfrac{1+tan^2x}{tan^2x}\)
\(=\dfrac{cot^2x}{\dfrac{1}{sin^2x}}\cdot\dfrac{\dfrac{1}{cos^2x}}{tan^2x}\)
\(=\dfrac{cot^2x}{tan^2x}\cdot\dfrac{1}{cos^2x}:\dfrac{1}{sin^2x}\)
\(=\dfrac{cot^2x}{tan^2x}\cdot\dfrac{sin^2x}{cos^2x}\)
\(=cot^2x\)
\(VP=\dfrac{tan^2x+cot^2x}{1+tan^4x}=\dfrac{\dfrac{sin^2x}{cos^2x}+\dfrac{cos^2x}{sin^2x}}{1+\dfrac{sin^4x}{cos^4x}}\)
\(=\dfrac{sin^4x+cos^4x}{sin^2x\cdot cos^2x}:\dfrac{cos^4x+sin^4x}{cos^4x}\)
\(=\dfrac{sin^4x+cos^4x}{sin^2x\cdot cos^2x}\cdot\dfrac{cos^4x}{cos^4x+sin^4x}=\dfrac{cos^2x}{sin^2x}=cot^2x\)
=>VT=VP
b:
\(\dfrac{tan^2x-cos^2x}{sin^2x}+\dfrac{cot^2x-sin^2x}{cos^2x}\)
\(=\dfrac{\left(\dfrac{sinx}{cosx}\right)^2-cos^2x}{sin^2x}+\dfrac{\left(\dfrac{cosx}{sinx}\right)^2-sin^2x}{cos^2x}\)
\(=\dfrac{sin^2x-cos^4x}{cos^2x\cdot sin^2x}+\dfrac{cos^2x-sin^4x}{sin^2x\cdot cos^2x}\)
\(=\dfrac{sin^2x+cos^2x-cos^4x-sin^4x}{cos^2x\cdot sin^2x}\)
\(=\dfrac{1-\left(cos^2x+sin^2x\right)^2+2\cdot cos^2x\cdot sin^2x}{cos^2x\cdot sin^2x}\)
\(=\dfrac{2\cdot cos^2x\cdot sin^2x}{cos^2x\cdot sin^2x}=2\)
Đúng 1
Bình luận (0)
Nghiệm của phương trình
c
o
t
3
x
-
1
là
Đọc tiếp
Nghiệm của phương trình c o t 3 x = - 1 là
![]()
![]()
![]()
![]()