Phân tích một vec tơ theo hai véc tơ không cùng phương cho trước
Những câu hỏi liên quan
cho AM , BN là hai trung tuyến của tam giác ABC . Hãy phân tích véc tơ BC
theo hai vec tơ AM và BN
Do BN là trung tuyến
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\\\overrightarrow{BN}=\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{BC}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}\\2\overrightarrow{BN}=\overrightarrow{BA}+\overrightarrow{BC}\end{matrix}\right.\)
Cộng vế với vế:
\(\overrightarrow{AM}+2\overrightarrow{BN}=\dfrac{3}{2}\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{BC}=\dfrac{2}{3}\overrightarrow{AM}+\dfrac{4}{3}\overrightarrow{BN}\)
Đúng 1
Bình luận (0)
Trên mặt phẳng cho 2013 vec-tơ trong đó không có hai vec-tơ nào cùng phương. Biết rằng tổng của 2012 vec-tơ bất kỳ đều cùng phương với vec-tơ còn lại. chứng minh rằng tổng của 2013 vec-tơ đó bằng 0.
Cho hình bình hành ABCD. Gọi N là trung điểm cạnh CD. Trên cạnh AC lấy điểm M sao cho AM = 2MC; Phân tích các vec tơ sau theo hai véc tơ ABvà AD
a. vecto ac
b) vecto AM
c) vecto an
Lời giải:
a.
$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$ (tính chất hình bình hành)
b.
$\overrightarrow{AM}=\frac{2}{3}\overrightarrow{AC}=\frac{2}{3}(\overrightarrow{AB}+\overrightarrow{AD})$
c.
$\overrightarrow{AN}=\overrightarrow{AC}+\overrightarrow{CN}=\overrightarrow{AC}+\frac{1}{2}\overrightarrow{BA}$
$=\overrightarrow{AB}+\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}$
$=\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}$
Đúng 1
Bình luận (0)
Cho véc tơ
n
→
≠
0
→
và hai véc tơ không cùng phương
a
→
,
b
→
. Nếu véc tơ
n
→
vuông góc với
a
→
,
b
→
thì ba véc tơ
n
→
,
a...
Đọc tiếp
Cho véc tơ n → ≠ 0 → và hai véc tơ không cùng phương a → , b → . Nếu véc tơ n → vuông góc với a → , b → thì ba véc tơ n → , a → , b →
A. Đồng phẳng.
B. Có thể đồng phẳng.
C. Có thể không đồng phẳng.
D. Không đồng phẳng.
Trong không gian với hệ tọa độ Oxyz, cho véc-tơ (1;0;-2). Trong các véc-tơ sau đây, véc-tơ nào không cùng phương với véc-tơ ?
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho véc-tơ 
=(1;0;-2). Trong các véc-tơ sau đây, véc-tơ nào không cùng phương với véc-tơ 
?
Trên đường thẳng chứa cạnh BC của tam giác ABC lấy điểm M sao cho . Hãy phân tích vec tơ theo hai vec tơ
Đọc tiếp
Trên đường thẳng chứa cạnh BC của tam giác ABC lấy điểm M sao cho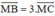 
. Hãy phân tích vec tơ 
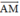theo hai vec tơ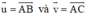 
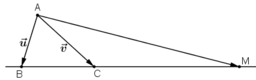
Ta có: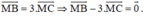 
Theo quy tắc ba điểm ta có:
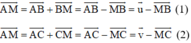
Lấy (1) trừ 3 lần (2) ta được:
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
P
:
x
+
2
y
+
z
−
4
0
. Trong các vec tơ sau vec tơ nào không phải là véc tơ pháp tuyến của (P)? A.
n
→
−
1
;
−
2
;...
Đọc tiếp
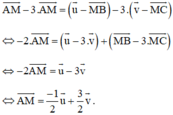
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : x + 2 y + z − 4 = 0 . Trong các vec tơ sau vec tơ nào không phải là véc tơ pháp tuyến của (P)?
A. n → = − 1 ; − 2 ; 1
B. n → = 1 ; 2 ; 1
C. n → = − 2 ; − 4 ; − 2
D. n → = 1 2 ; 1 ; 1 2
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x+2y+z-40. Trong các vec tơ sau vec tơ nào không phải là véc tơ pháp tuyến của (P)? A.
n
→
-
1
;
-
2
;
1
B.
n...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x+2y+z-4=0. Trong các vec tơ sau vec tơ nào không phải là véc tơ pháp tuyến của (P)?
A. n → = - 1 ; - 2 ; 1
B. n → = 1 ; 2 ; 1
C. n → = - 2 ; - 4 ; - 2
D. n → = 1 2 ; 1 ; 1 2
Cho tam giác ABC và M là trung điểm BC. Phân tích vec tơ AM theo vec tơ BA và vec tơ CA