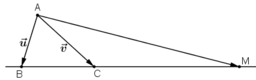
Ta có: 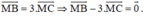
Theo quy tắc ba điểm ta có:
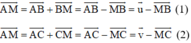
Lấy (1) trừ 3 lần (2) ta được:
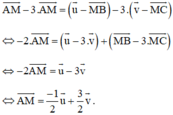

Ta có: 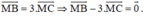
Theo quy tắc ba điểm ta có:
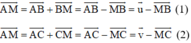
Lấy (1) trừ 3 lần (2) ta được:
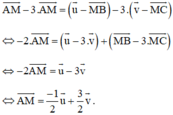
Cho tam giác ABC và M là trung điểm BC. Phân tích vec tơ AM theo vec tơ BA và vec tơ CA
Cho AK và BM là hai trung tuyến của tam giác ABC. Hãy phân tích các vectơ 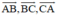 theo hai vec tơ
theo hai vec tơ 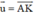 và
và 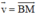
cho tam giác abc. Gọi M, N là các điểm thoả mãn: vecBM=3/4vecBC, vecBN=1/4vecBA
a. Phân tích vecAB theo vecAC và vecMN
b. Gọi E là trung điểm MN. Phân tích vecAE theo hai vec AB và AC
c. Lấy F là điểm trên BC sao cho BE=mBC. Tìm m để 3 điểm A, E, F thẳng hàng
Bài 4. Cho tam giác ABC có AM là đường trung tuyến và D là trung điểm của AM. a) Chứng minh rằng: 2 vec DA + vec DB + vec DC = vec 0 b) Chứng minh rằng: vec BD = 1 2 vec B vec A + 1 4 vec BC . c) Gọi E là điểm trên cạnh AC sao cho AE = 1/3 * A * C Chứng minh rằng B, D, E thẳng hàng. Tính tỉ số (DB)/(DE)
Câu 1: Cho tam giác đều ABC có cạnh là 10a, M là trung điểm của BC. Tính | vec AB + vec AM | ? vec AM . vec BA ? Câu 2: Cho tam giác ABC vuông tại A có AB = 2a căn 3 ; AC = 2a . Tính ? vec AB . vec BC ; | vec AB - vec AC |
Cho hình bình hành ABCD tâm O. Gọi M, N lần lượt là trung điểm của BC, CD; G là trọng tâm tam giác ABC.
a) Chứng minh AM + AN = 3/2 AC và GA +3GB+GC+GD=0
c) Gọi I là điểm thỏa mãn AI= 3/4AB. Phân tích IN ; IG theo hai vec tơ BA và BC
Chứng minh 3 điểm N;G;I thẳng hàng.
Cho hai vec tơ ![]() và {\displaystyle {\vec {d}}}
và {\displaystyle {\vec {d}}}![]() đều khác
đều khác ![]() Gọi
Gọi ![]() là góc giữa hai vec tơ đó.
là góc giữa hai vec tơ đó.
Ta có ![]()
Cho tam giác ABC có AB=4, AC = 5 , BAC =120°. G là trọng tâm của tam giác ABC, điểm E thỏa mãn vector AE=2/3 vector EC
a) Biểu diễn BE theo AB,AC.
b) Tìm tập hợp điểm I thỏa mãn đẳng thức vec tơ |IA+IG|=|IA–IG|.
c) M là một điểm khác G thỏa(GC-GB)(MA+MB+MC)=0. Chứng minh MG vg BC.
vector het nha