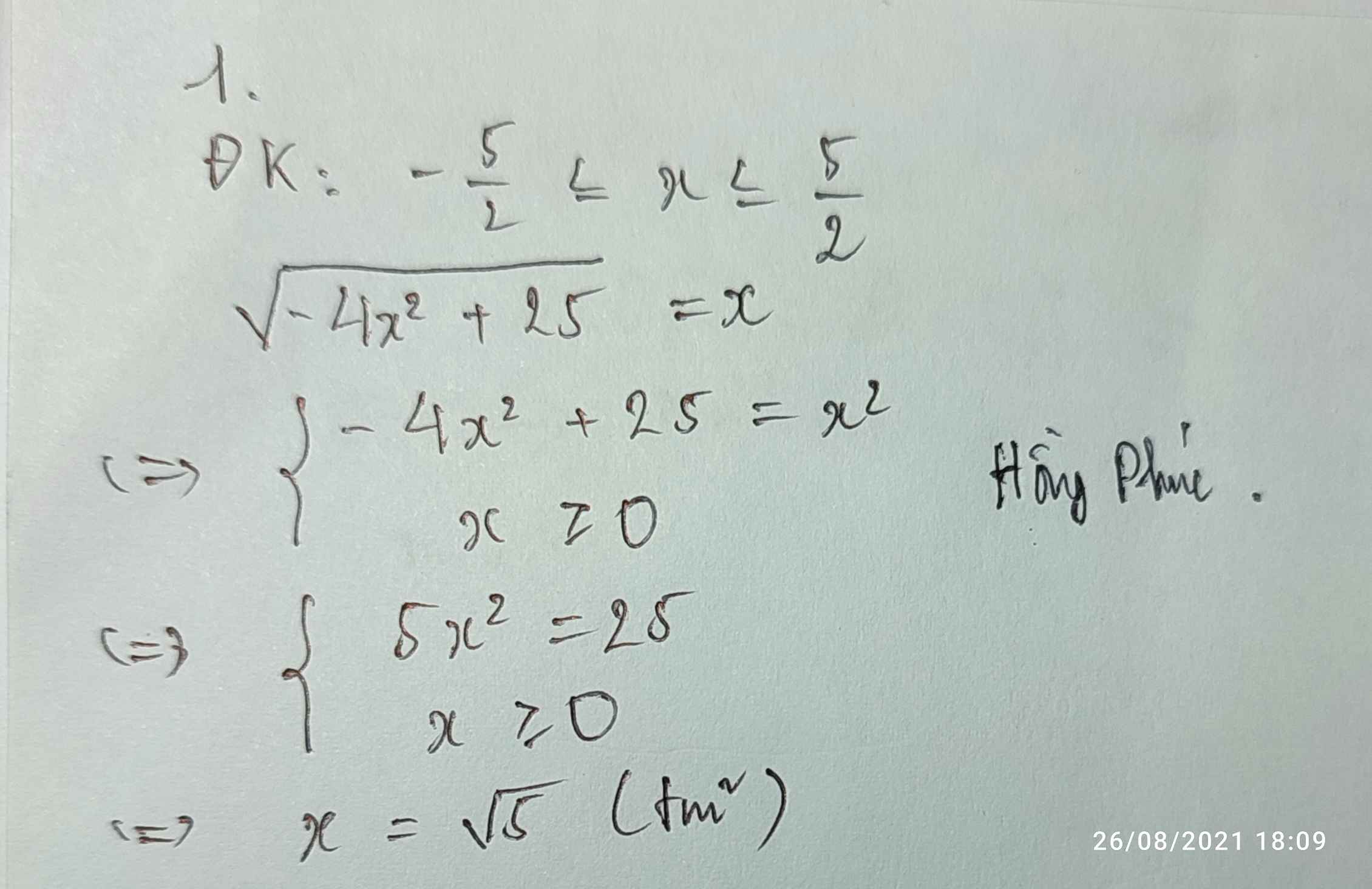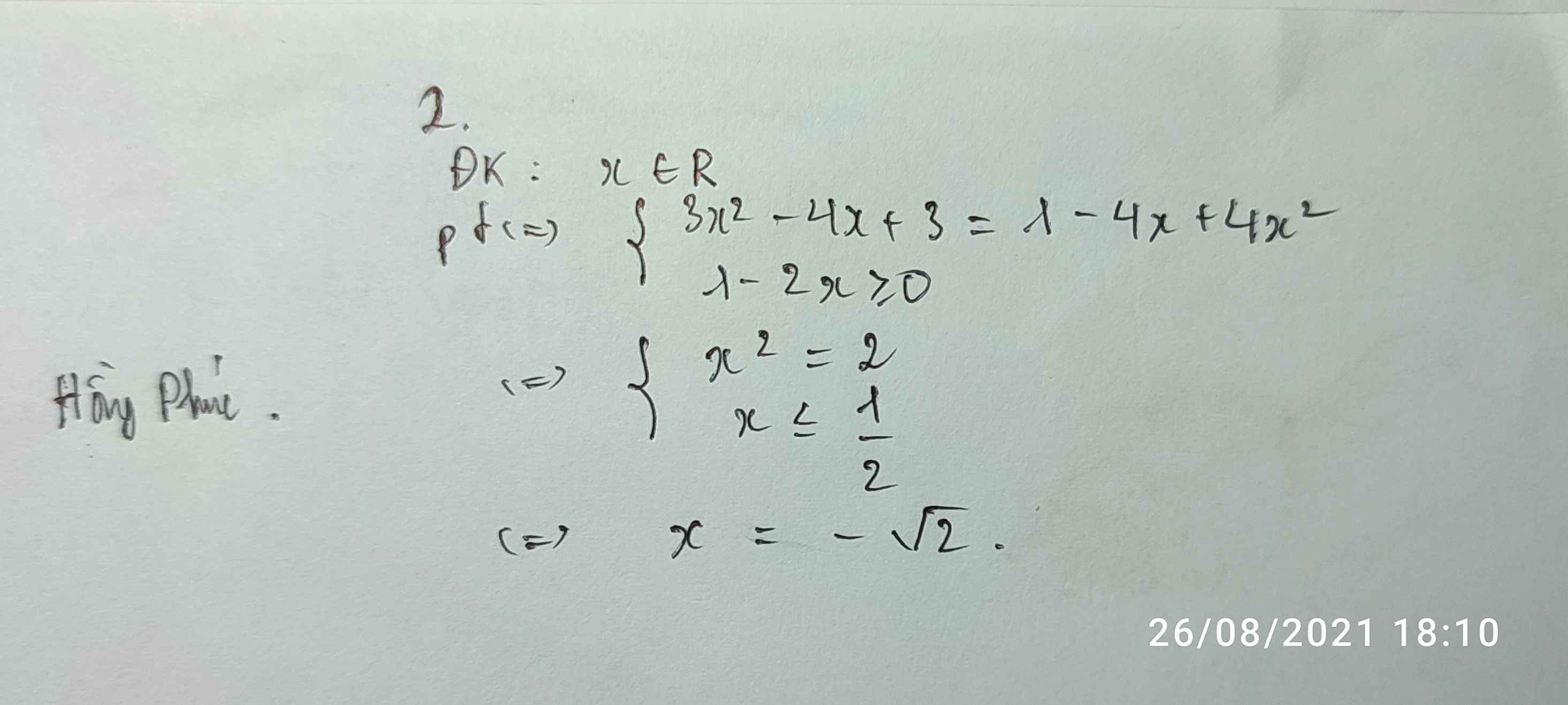c: Ta có: \(\sqrt{x-1}+\sqrt{9x-9}-\sqrt{4x-4}=4\)

\(\Leftrightarrow2\sqrt{x-1}=4\)

\(\Leftrightarrow x-1=4\)

hay x=5

e: Ta có: \(\sqrt{4x^2-28x+49}-5=0\)

\(\Leftrightarrow\left|2x-7\right|=5\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-7=5\\2x-7=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=1\end{matrix}\right.\)

a. ĐKXĐ: $x\in\mathbb{R}$

PT $\Leftrightarrow \sqrt{(x-2)^2}=2-x$

$\Leftrightarrow |x-2|=2-x$
$\Leftrightarrow 2-x\geq 0$

$\Leftrightarrow x\leq 2$

b. ĐKXĐ: $x\geq 2$

PT $\Leftrightarrow \sqrt{4}.\sqrt{x-2}-\frac{1}{5}\sqrt{25}.\sqrt{x-2}=3\sqrt{x-2}-1$

$\Leftrightarrow 2\sqrt{x-2}-\sqrt{x-2}=3\sqrt{x-2}-1$

$\Leftrightarrow 1=2\sqrt{x-2}$

$\Leftrightarrow \frac{1}{2}=\sqrt{x-2}$

$\Leftrightarrow \frac{1}{4}=x-2$

$\Leftrightarrow x=\frac{9}{4}$ (tm)

c. ĐKXĐ: $x\geq 1$

PT $\Leftrightarrow \sqrt{x-1}+\sqrt{9}.\sqrt{x-1}-\sqrt{4}.\sqrt{x-1}=4$

$\Leftrightarrow \sqrt{x-1}+3\sqrt{x-1}-2\sqrt{x-1}=4$

$\Leftrightarrow 2\sqrt{x-1}=4$

$\Leftrightarrow \sqrt{x-1}=2$

$\Leftrightarrow x-1=4$

$\Leftrightarrow x=5$ (tm)

d. ĐKXĐ: $x\geq 2$

PT $\Leftrightarrow \frac{1}{2}\sqrt{x-2}-4\sqrt{\frac{4}{9}}\sqrt{x-2}+\sqrt{9}.\sqrt{x-2}-5=0$

$\Leftrightarrow \frac{1}{2}\sqrt{x-2}-\frac{8}{3}\sqrt{x-2}+3\sqrt{x-2}-5=0$

$\Leftrightarrow \frac{5}{6}\sqrt{x-2}-5=0$

$\Leftrightarrow \sqrt{x-2}=6$

$\Leftrightarrow x-2=36$

$\Leftrightarrow x=38$ (tm)

a: ta có: \(\sqrt{x-1}+\sqrt{4x-4}-\sqrt{25x-25}+2=0\)

\(\Leftrightarrow\sqrt{x-1}+2\sqrt{x-1}-5\sqrt{x-1}+2=0\)

\(\Leftrightarrow\sqrt{x-1}=1\)

hay x=2

c: Ta có: \(\sqrt{1-2x^2}=x-1\)

\(\Leftrightarrow1-2x^2=x^2-2x+1\)

\(\Leftrightarrow-3x^2+2x=0\)

\(\Leftrightarrow-x\left(3x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=\dfrac{2}{3}\left(loại\right)\end{matrix}\right.\)

1) \(\sqrt[]{9\left(x-1\right)}=21\)

\(\Leftrightarrow9\left(x-1\right)=21^2\)

\(\Leftrightarrow9\left(x-1\right)=441\)

\(\Leftrightarrow x-1=49\Leftrightarrow x=50\)

2) \(\sqrt[]{1-x}+\sqrt[]{4-4x}-\dfrac{1}{3}\sqrt[]{16-16x}+5=0\)

\(\Leftrightarrow\sqrt[]{1-x}+\sqrt[]{4\left(1-x\right)}-\dfrac{1}{3}\sqrt[]{16\left(1-x\right)}+5=0\)

\(\)\(\Leftrightarrow\sqrt[]{1-x}+2\sqrt[]{1-x}-\dfrac{4}{3}\sqrt[]{1-x}+5=0\)

\(\Leftrightarrow\sqrt[]{1-x}\left(1+3-\dfrac{4}{3}\right)+5=0\)

\(\Leftrightarrow\sqrt[]{1-x}.\dfrac{8}{3}=-5\)

\(\Leftrightarrow\sqrt[]{1-x}=-\dfrac{15}{8}\)

mà \(\sqrt[]{1-x}\ge0\)

\(\Leftrightarrow pt.vô.nghiệm\)

3) \(\sqrt[]{2x}-\sqrt[]{50}=0\)

\(\Leftrightarrow\sqrt[]{2x}=\sqrt[]{50}\)

\(\Leftrightarrow2x=50\Leftrightarrow x=25\)

1) \(\sqrt{9\left(x-1\right)}=21\) (ĐK: \(x\ge1\))

\(\Leftrightarrow3\sqrt{x-1}=21\)

\(\Leftrightarrow\sqrt{x-1}=7\)

\(\Leftrightarrow x-1=49\)

\(\Leftrightarrow x=49+1\)

\(\Leftrightarrow x=50\left(tm\right)\)

2) \(\sqrt{1-x}+\sqrt{4-4x}-\dfrac{1}{3}\sqrt{16-16x}+5=0\) (ĐK: \(x\le1\))

\(\Leftrightarrow\sqrt{1-x}+2\sqrt{1-x}-\dfrac{4}{3}\sqrt{1-x}+5=0\)

\(\Leftrightarrow\dfrac{5}{3}\sqrt{1-x}+5=0\)

\(\Leftrightarrow\dfrac{5}{3}\sqrt{1-x}=-5\) (vô lý) 

Phương trình vô nghiệm

3) \(\sqrt{2x}-\sqrt{50}=0\) (ĐK: \(x\ge0\)) 

\(\Leftrightarrow\sqrt{2x}=\sqrt{50}\)

\(\Leftrightarrow2x=50\)

\(\Leftrightarrow x=\dfrac{50}{2}\)

\(\Leftrightarrow x=25\left(tm\right)\)

4) \(\sqrt{4x^2+4x+1}=6\)

\(\Leftrightarrow\sqrt{\left(2x+1\right)^2}=6\)

\(\Leftrightarrow\left|2x+1\right|=6\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+1=6\left(ĐK:x\ge-\dfrac{1}{2}\right)\\2x+1=-6\left(ĐK:x< -\dfrac{1}{2}\right)\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=5\\2x=-7\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\left(tm\right)\\x=-\dfrac{7}{2}\left(tm\right)\end{matrix}\right.\)

5) \(\sqrt{\left(x-3\right)^2}=3-x\)

\(\Leftrightarrow\left|x-3\right|=3-x\)

\(\Leftrightarrow x-3=3-x\)

\(\Leftrightarrow x+x=3+3\)

\(\Leftrightarrow x=\dfrac{6}{2}\)

\(\Leftrightarrow x=3\)

1) => 9(x-1)=\(21^2\)

=> 9x-9=441

=> 9x=450

=> x=50

2)=>\(\sqrt{1-x}\) + \(\sqrt{4\left(1-x\right)}\)-\(\dfrac{1}{3}\sqrt{16\left(1-x\right)}\)+5=0

=>\(\sqrt{1-x}\)\(\left(1+2-\dfrac{1}{3}.4\right)\)+5=0

=>\(\dfrac{5}{3}\sqrt{1-x}\) +5=0

=>\(\sqrt{1-x}\)=-3

Phuong trinh vo nghiem

a, ĐKXĐ: \(x^2-4x+4\ge0\Rightarrow\left(x-2\right)^2\ge0\left(luônđúng\right)\)

 \(\sqrt{x^2-4x+4}=1\\ \Rightarrow x-2=1\\ \Rightarrow x=3\)

b,\(ĐKXĐ:1-4x+4x^2\ge0\Rightarrow\left(1-2x\right)^2\ge0\left(luônđúng\right)\)

 \(\sqrt{1-4x+4x^2}=5\\ \Rightarrow\left|1-2x\right|=5\\ \Rightarrow\left[{}\begin{matrix}1-2x=5\\1-2x=-5\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-2\\x=3\end{matrix}\right.\)

d, ĐKXĐ: \(\left\{{}\begin{matrix}9x^2\ge0\\2x+1\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge0\\x\ge-\dfrac{1}{2}\end{matrix}\right.\Rightarrow x\ge0\)

\(\sqrt{9x^2}=2x+1\\ \Rightarrow\left|3x\right|=2x+1\\ \Rightarrow\left[{}\begin{matrix}3x=2x+1\\3x=-2x+1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{5}\end{matrix}\right.\)

c, ĐKXĐ: \(1-2x+x^2\ge0\Rightarrow\left(1-x\right)^2\ge0\left(luônđúng\right)\)

 \(\sqrt{1-2x+x^2}-6=0\\ \Rightarrow\left|1-x\right|=6\\ \Rightarrow\left[{}\begin{matrix}1-x=-6\\1-x=6\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=7\\x=-5\end{matrix}\right.\)

e, \(\left\{{}\begin{matrix}9-6x+x^2\ge0\\x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\left(3-x\right)^2\ge0\left(luônđúng\right)\\x\ge0\end{matrix}\right.\)\(\Rightarrow x\ge0\)

\(\sqrt{9-6x+x^2}=x\\ \Rightarrow\left|3-x\right|=x\\ \Rightarrow\left[{}\begin{matrix}3-x=-x\\3-x=x\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}3=0\left(vôlí\right)\\x=1,5\end{matrix}\right.\)

a) \(\sqrt{x^2-4x+4}=1\)

\(\Leftrightarrow\sqrt{\left(x-2\right)^2}=1\Leftrightarrow\left|x-2\right|=1\)

\(\Leftrightarrow\left[{}\begin{matrix}x-2=1\\x-2=-1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)

b) \(\sqrt{1-4x+4x^2}=5\)

\(\Leftrightarrow\sqrt{\left(1-2x\right)^2}=5\Leftrightarrow\left|1-2x\right|=5\)

\(\Leftrightarrow\left[{}\begin{matrix}1-2x=5\\1-2x=-5\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=3\end{matrix}\right.\)

c) \(\sqrt{x\left(1-2x+x^2\right)}-6=0\)

\(\Leftrightarrow\left(\sqrt{x\left(1-x\right)^2}\right)^2=36\Leftrightarrow x\left(1-x\right)^2=36\)

\(\Leftrightarrow x-2x^2+x^3-36=0\)

\(\Leftrightarrow\left(x-4\right)\left(x^2+2x+9\right)=0\)

\(\Leftrightarrow x=4\)(do \(x^2+2x+9=\left(x+1\right)^2+8>0\))

d) \(\sqrt{9x^2}=2x+1\)

\(\Leftrightarrow3\left|x\right|=2x+1\)

\(\Leftrightarrow\left[{}\begin{matrix}3x=2x+1\\-3x=2x+1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{5}\end{matrix}\right.\)

e) \(\sqrt{9-6x+x^2}=x\left(1\right)\left(đk:x\ge0\right)\)

\(\Leftrightarrow\sqrt{\left(3-x\right)^2}=x\Leftrightarrow\left|3-x\right|=x\)

TH1: \(0\le x\le3\)

\(\left(1\right)\Leftrightarrow3-x=x\Leftrightarrow x=\dfrac{3}{2}\)

TH2: \(x>3\)

\(\left(1\right)\Leftrightarrow x-3=x\Leftrightarrow-3=0\left(vn\right)\)

1.

\(x^4-6x^2-12x-8=0\)

\(\Leftrightarrow x^4-2x^2+1-4x^2-12x-9=0\)

\(\Leftrightarrow\left(x^2-1\right)^2=\left(2x+3\right)^2\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2-1=2x+3\\x^2-1=-2x-3\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x-4=0\\x^2+2x+2=0\end{matrix}\right.\)

\(\Leftrightarrow x=1\pm\sqrt{5}\)

3.

ĐK: \(x\ge-9\)

\(x^4-x^3-8x^2+9x-9+\left(x^2-x+1\right)\sqrt{x+9}=0\)

\(\Leftrightarrow\left(x^2-x+1\right)\left(\sqrt{x+9}+x^2-9\right)=0\)

\(\Leftrightarrow\sqrt{x+9}+x^2-9=0\left(1\right)\)

Đặt \(\sqrt{x+9}=t\left(t\ge0\right)\Rightarrow9=t^2-x\)

\(\left(1\right)\Leftrightarrow t+x^2+x-t^2=0\)

\(\Leftrightarrow\left(x+t\right)\left(x-t+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-t\\x=t-1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\sqrt{x+9}\\x=\sqrt{x+9}-1\end{matrix}\right.\)

\(\Leftrightarrow...\)

2.

ĐK: \(x\ne\dfrac{2\pm\sqrt{2}}{2};x\ne\dfrac{-2\pm\sqrt{2}}{2}\)

\(\dfrac{x}{2x^2+4x+1}+\dfrac{x}{2x^2-4x+1}=\dfrac{3}{5}\)

\(\Leftrightarrow\dfrac{1}{2x+\dfrac{1}{x}+4}+\dfrac{1}{2x+\dfrac{1}{x}-4}=\dfrac{3}{5}\)

Đặt \(2x+\dfrac{1}{x}+4=a;2x+\dfrac{1}{x}-4=b\left(a,b\ne0\right)\)

\(pt\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{3}{5}\left(1\right)\)

Lại có \(a-b=8\Rightarrow a=b+8\), khi đó:

\(\left(1\right)\Leftrightarrow\dfrac{1}{b+8}+\dfrac{1}{b}=\dfrac{3}{5}\)

\(\Leftrightarrow\dfrac{2b+8}{\left(b+8\right)b}=\dfrac{3}{5}\)

\(\Leftrightarrow10b+40=3\left(b+8\right)b\)

\(\Leftrightarrow\left[{}\begin{matrix}b=2\\b=-\dfrac{20}{3}\end{matrix}\right.\)

TH1: \(b=2\Leftrightarrow...\)

TH2: \(b=-\dfrac{20}{3}\Leftrightarrow...\)

1) \(\sqrt{5-2x}=6\left(đk:x\le\dfrac{5}{2}\right)\)

\(\Leftrightarrow5-2x=36\)

\(\Leftrightarrow2x=-31\Leftrightarrow x=-\dfrac{31}{2}\left(tm\right)\)

2) \(\sqrt{2-x}=\sqrt{x+1}\left(đk:2\ge x\ge-1\right)\)

\(\Leftrightarrow2-x=x+1\)

\(\Leftrightarrow2x=1\Leftrightarrow x=\dfrac{1}{2}\left(tm\right)\)

3) \(\Leftrightarrow\sqrt{\left(2x+1\right)^2}=6\)

\(\Leftrightarrow\left|2x+1\right|=6\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+1=6\\2x+1=-6\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{7}{2}\end{matrix}\right.\)

4) \(\sqrt{x^2-10x+25}=x-2\left(đk:x\ge2\right)\)

\(\Leftrightarrow\sqrt{\left(x-5\right)^2}=x-2\)

\(\Leftrightarrow\left|x-5\right|=x-2\)

\(\Leftrightarrow\left[{}\begin{matrix}x-5=x-2\left(x\ge5\right)\\x-5=2-x\left(2\le x< 5\right)\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}5=2\left(VLý\right)\\x=\dfrac{7}{2}\left(tm\right)\end{matrix}\right.\)

\(a,đk:x\ge5\\ \Leftrightarrow\sqrt{x-5}+\sqrt{4\left(x-5\right)}-\dfrac{1}{5}\sqrt{9\left(x-5\right)}=3\\ \Leftrightarrow\sqrt{x-5}+2\sqrt{x-5}-\dfrac{1}{5}.3\sqrt{x-5}=3\\ \Leftrightarrow\dfrac{12}{5}\sqrt{x-5}=3\\ \Rightarrow\sqrt{x-5}=\dfrac{5}{4}\\ \Leftrightarrow\left(\sqrt{x-5}\right)^2=\left(\dfrac{5}{4}\right)^2\\ \Leftrightarrow x-5=\dfrac{25}{16}\\ \Rightarrow x=\dfrac{25}{16}+5\\ \Rightarrow x=\dfrac{105}{16}\left(t|m\right)\)

\(b,đk:x\ge1\\ \Leftrightarrow\sqrt{x-1}+\sqrt{4\left(x-1\right)}-\sqrt{25\left(x-1\right)}=-2\\ \Leftrightarrow\sqrt{x-1}+2\sqrt{x-1}-5\sqrt{x-1}=-2\\ \Leftrightarrow-2\sqrt{x-1}=-2\\ \Leftrightarrow\sqrt{x-1}=1\\ \Leftrightarrow x-1=1\\ \Leftrightarrow x=2\left(t|m\right)\)

\(d,ĐK:x\ge0\\ PT\Leftrightarrow\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=2\\\sqrt{x}=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\x=9\left(tm\right)\end{matrix}\right.\\ e,ĐK:x\ge1\\ PT\Leftrightarrow\sqrt{x-1}+\dfrac{3}{2}\cdot2\sqrt{x-1}-\dfrac{2}{5}\cdot5\sqrt{x-1}=4\\ \Leftrightarrow2\sqrt{x-1}=4\Leftrightarrow\sqrt{x-1}=2\\ \Leftrightarrow x-1=4\Leftrightarrow x=5\left(tm\right)\\ f,ĐK:x\ge5\\ PT\Leftrightarrow\sqrt{x-5}+2\sqrt{x-5}-\dfrac{1}{3}\cdot3\sqrt{x-5}=6\\ \Leftrightarrow2\sqrt{x-5}=6\Leftrightarrow\sqrt{x-5}=3\\ \Leftrightarrow x-5=9\Leftrightarrow x=14\left(tm\right)\)

a) \(\sqrt{x^2+2x+1}=9\)

\(\Leftrightarrow\sqrt{\left(\sqrt{x}+1\right)^2}=9\)

\(\Leftrightarrow\left|\sqrt{x}+1\right|=9\)

\(\Leftrightarrow\left[{}\begin{matrix}x+1=9\\x+1=-9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-10\end{matrix}\right.\)

b)\(\sqrt{1-4x+4x^2}=5\)

\(\Leftrightarrow\sqrt{\left(1-2x\right)^2}=5\)

\(\Leftrightarrow\left|1-2x\right|=5\)

\(\Leftrightarrow\left[{}\begin{matrix}1-2x=5\\1-2x=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=3\end{matrix}\right.\)

c)\(\sqrt{x^2-2x\sqrt{2}+2}=5\)

\(\Leftrightarrow\sqrt{\left(x-\sqrt{2}\right)^2}=5\)

\(\Leftrightarrow\left|x-\sqrt{2}\right|=5\)

\(\left[{}\begin{matrix}x-\sqrt{2}=5\\x-\sqrt{2}=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5+\sqrt{2}\\x=-5+\sqrt{2}\end{matrix}\right.\)

Mình giải tới đây thôi