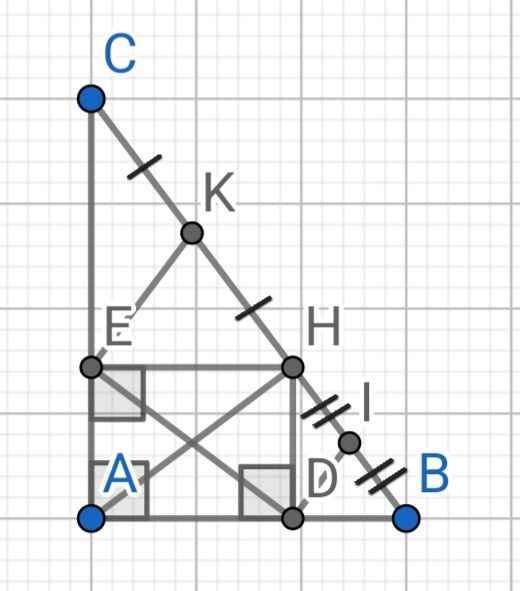
Cho tam giác ABC vuông tại A. AH là đường cao . Qua H kẻ các đường thẳng vuông góc với AB tại E, vuông góc với Ac tại F.
Gọi O là trung điểm của AH. Gọi M là trung điểm của HC. Kẻ MI song song với AH ( I thuộc AC ) Gọi K là điểm đối xứng của I qua M
a) Tính độ dài Hi biết AC = 5cm
b) CM HICK là hình thoi
c) CM BO vuông góc với Am