a/ \(sin3x=sin\left(2x+x\right)=sin2xcosx+cos2x.sinx\)

\(=2sinxcos^2x+\left(1-2sin^2x\right)sinx=2sinx\left(1-sin^2x\right)+sinx-2sin^3x\)

\(=3sinx-4sin^3x\)

b/

\(tan2x+\frac{1}{cos2x}=\frac{sin2x}{cos2x}+\frac{1}{cos2x}=\frac{sin2x+1}{cos2x}=\frac{2sinxcosx+sin^2x+cos^2x}{cos^2x-sin^2x}\)

\(=\frac{\left(sinx+cosx\right)^2}{\left(sinx+cosx\right)\left(cosx-sinx\right)}=\frac{sinx+cosx}{cosx-sinx}=\frac{\left(sinx+cosx\right)\left(cosx-sinx\right)}{\left(cos-sinx\right)^2}\)

\(=\frac{cos^2x-sin^2x}{cos^2x+sin^2x-2sinxcosx}=\frac{1-2sin^2x}{1-sin2x}\)

c/

\(\frac{cosx+sinx}{cosx-sinx}-\frac{cosx-sinx}{cosx+sinx}=\frac{\left(cosx+sinx\right)^2-\left(cosx-sinx\right)^2}{cos^2x-sin^2x}\)

\(=\frac{2sinxcosx+2sinxcosx}{cos2x}=\frac{4sinxcosx}{cos2x}=\frac{2sin2x}{cos2x}=2tan2x\)

d/

\(\frac{sin2x}{1+cos2x}=\frac{2sinxcosx}{1+2cos^2x-1}=\frac{2sinxcosx}{2cos^2x}=\frac{sinx}{cosx}=tanx\)

e/

1: =>sin^2(3x)=0

=>sin 3x=0

=>3x=kpi

=>x=kpi/3

2:

\(sinx=1-cos^2x=sin^2x\)

=>\(sin^2x-sinx=0\)

=>sin x(sin x-1)=0

=>sin x=0 hoặc sin x=1

=>x=pi/2+k2pi hoặc x=kpi

4:

sin 2x+sin x=0

=>sin 2x=-sin x=sin(-x)

=>2x=-x+k2pi hoặc 2x=pi+x+k2pi

=>x=pi+k2pi hoặc x=k2pi/3

5: =>cos(x+pi/3)=1/căn 2

=>x+pi/3=pi/4+k2pi hoặc x+pi/3=-pi/4+k2pi

=>x=-pi/12+k2pi hoặc x=-7/12pi+k2pi

Đặt t = sin x − cos x = 2 sin x − π 4 .

Điều kiện  −   2 ≤ t ≤ 2 .

Ta có  t 2 = sin x − cos x 2 = sin 2 x + cos 2 x − 2 sin x cos x ⇒ sin 2 x = 1 − t 2 .

Phương trình đã cho trở thành 1 − t 2 + t = 1 ⇔ t 2 − t = 0 ⇔ t = 0 t = 1 .

Với t = 1, ta được  2 sin x − π 4 = 1 ⇔ sin x − π 4 = 1 2 .

Với t = 0, ta được  2 sin x − π 4 = 0 ⇔ sin x − π 4 = 0.

Chọn đáp án B.

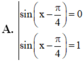
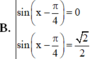
Chọn B

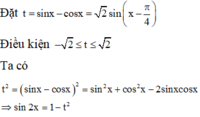
Bổ trợ kiến thức: Ta có thế giải bằng máy tính cầm tay CASIO fx-570VN PLUS như sau, đâu tiên dùng lệnh SHIFT SOLVE để xem 1 nghiệm bất kì có thể có của phương trình đã cho:

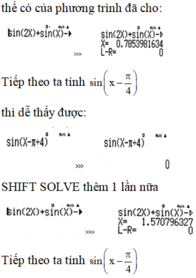
Đến đây ta dễ dàng chọn được phương án B là phương án đúng thay cho lời giải tự luận nhiều phức tạp.

1.

\(2sin\left(x+\dfrac{\pi}{6}\right)+sinx+2cosx=3\)

\(\Leftrightarrow\sqrt{3}sinx+cosx+sinx+2cosx=3\)

\(\Leftrightarrow\left(\sqrt{3}+1\right)sinx+3cosx=3\)

\(\Leftrightarrow\sqrt{13+2\sqrt{3}}\left[\dfrac{\sqrt{3}+1}{\sqrt{13+2\sqrt{3}}}sinx+\dfrac{3}{\sqrt{13+2\sqrt{3}}}cosx\right]=3\)

Đặt \(\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)

\(pt\Leftrightarrow\sqrt{13+2\sqrt{3}}sin\left(x+\alpha\right)=3\)

\(\Leftrightarrow sin\left(x+\alpha\right)=\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)

\(\Leftrightarrow\left[{}\begin{matrix}x+\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\\x+\alpha=\pi-arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)

Vậy phương trình đã cho có nghiệm:

\(x=k2\pi;x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\)

2.

\(\left(sin2x+cos2x\right)cosx+2cos2x-sinx=0\)

\(\Leftrightarrow2sinx.cos^2x+cos2x.cosx+2cos2x-sinx=0\)

\(\Leftrightarrow\left(2cos^2x-1\right)sinx+cos2x.cosx+2cos2x=0\)

\(\Leftrightarrow cos2x.sinx+cos2x.cosx+2cos2x=0\)

\(\Leftrightarrow cos2x.\left(sinx+cosx+2\right)=0\)

\(\Leftrightarrow cos2x=0\)

\(\Leftrightarrow2x=\dfrac{\pi}{2}+k\pi\)

\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)

Vậy phương trình đã cho có nghiệm \(x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)

1.

\(\Leftrightarrow4sinx.cosx+3\left(sinx-cosx\right)=0\)

Đặt \(sinx-cosx=t\Rightarrow\left\{{}\begin{matrix}\left|t\right|\le\sqrt{2}\\2sinx.cosx=1-t^2\end{matrix}\right.\)

Pt trở thành:

\(2\left(1-t^2\right)+3t=0\)

\(\Leftrightarrow-2t^2+3t+2=0\Rightarrow\left[{}\begin{matrix}t=2\left(l\right)\\t=-\frac{1}{2}\end{matrix}\right.\)

\(\Leftrightarrow sinx-cosx=-\frac{1}{2}\)

\(\Leftrightarrow\sqrt{2}sin\left(x-\frac{\pi}{4}\right)=-\frac{1}{2}\)

\(\Leftrightarrow sin\left(x-\frac{\pi}{4}\right)=-\frac{1}{2\sqrt{2}}\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+arcsin\left(-\frac{1}{2\sqrt{2}}\right)+k2\pi\\x=\frac{5\pi}{4}-arcsin\left(-\frac{1}{2\sqrt{2}}\right)+k2\pi\end{matrix}\right.\)

2.

Đặt \(sinx-cosx=t\Rightarrow\left\{{}\begin{matrix}\left|t\right|\le\sqrt{2}\\sin2x=2sinx.cosx=1-t^2\end{matrix}\right.\)

Pt trở thành:

\(1-t^2-4t=4\)

\(\Leftrightarrow t^2+4t+3=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=-3\left(l\right)\end{matrix}\right.\)

\(\Rightarrow sinx-cosx=-1\)

\(\Leftrightarrow\sqrt{2}sin\left(x-\frac{\pi}{4}\right)=-1\)

\(\Leftrightarrow sin\left(x-\frac{\pi}{4}\right)=-\frac{\sqrt{2}}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}x-\frac{\pi}{4}=-\frac{\pi}{4}+k2\pi\\x-\frac{\pi}{4}=\frac{5\pi}{4}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\frac{3\pi}{2}+k2\pi\end{matrix}\right.\)

3.

\(\Leftrightarrow1+cosx+sinx+sinx.cosx=2\)

\(\Leftrightarrow2\left(sinx+cosx\right)+2sinx.cosx-2=0\)

Đặt \(sinx+cosx=t\Rightarrow\left\{{}\begin{matrix}\left|t\right|\le\sqrt{2}\\2sinx.cosx=t^2-1\end{matrix}\right.\)

Pt trở thành:

\(2t+t^2-1-2=0\)

\(\Leftrightarrow t^2+2t-3=0\Rightarrow\left[{}\begin{matrix}t=1\\t=-3\left(l\right)\end{matrix}\right.\)

\(\Leftrightarrow sinx+cosx=1\)

\(\Leftrightarrow\sqrt{2}sin\left(x+\frac{\pi}{4}\right)=1\)

\(\Leftrightarrow sin\left(x+\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}x+\frac{\pi}{4}=\frac{\pi}{4}+k2\pi\\x+\frac{\pi}{4}=\frac{3\pi}{4}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\frac{\pi}{2}+k2\pi\end{matrix}\right.\)