Tìm giá trị chính xác của:
a/ \(4x^3-3x-\frac{\sqrt{6}+\sqrt{2}}{4}=0\)
b/ \(-4x^3+3x-sin\left(15^o\right)=0\)
Xin cách giải chi tiết ạ
Bài 1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0 ĐẾN 180 ĐỘ
Sử dụng kiến thức lớp 10 thì không được đâu bạn
Bài này cần công thức lượng giác của lớp 11 để giải ra kết quả chính xác
Đúng 0
Bình luận (0)
Tìm giá trị max của biểu thức P=cos^4-cos^2+sin^2x
Xem chi tiết
\(P=cos^4x-cos^2x+sin^2x\) đúng ko bạn?
\(P=\left(\dfrac{1+cos2x}{2}\right)^2-cos2x\)
\(P=\dfrac{1}{4}cos^22x-\dfrac{1}{2}cos2x+\dfrac{1}{4}\)
\(P=\dfrac{1}{4}\left(cos^22x-2cos2x-3\right)+1\)
\(P=\dfrac{\left(cos2x-3\right)\left(cos2x+1\right)}{4}+1\le1\)
\(P_{max}=1\) khi \(cos2x=-1\)
Đúng 1
Bình luận (0)
Cm rằng với mọi góc a ta luôn có cos^2a+sin^2a=1
Xem chi tiết
Tham khảo:
Chứng minh rằng với mọi góc α (00 ≤ α ≤ 1800) ta đều có cos2 α sin2 α = 1. - Hoc24
Đúng 0
Bình luận (0)
Cho cosa=1/3, 90°
Xem chi tiết
Cho tam giác ABC cân tại A góc BAC = 120° góc giữa vectơ AB và vectơ CA là
Xem chi tiết
Lời giải:
\(\cos (\overrightarrow{AB}, \overrightarrow{CA})=\frac{\overrightarrow{AB}.\overrightarrow{CA}}{|\overrightarrow{AB}||\overrightarrow{CA}|}=\frac{-\overrightarrow{AB}.\overrightarrow{AC}}{|\overrightarrow{AB}||\overrightarrow{AC}|}=-\cos (\overrightarrow{AB}, \overrightarrow{AC})=-\cos (120^0)=\frac{1}{2}\)
\(\Rightarrow \angle (\overrightarrow{AB}, \overrightarrow{CA})=60^0\)
Đúng 1
Bình luận (0)
Nêu đặc điểm của tam giác ABC biết \(\sin(A) * \cos^{2}(B) = \sin(B) * \cos^{2}(A)\)
\(sinA\left(1-sin^2B\right)=sinB\left(1-sin^2A\right)\)
\(\Leftrightarrow sinA-sinB-sinA.sin^2B+sin^2A.sinB=0\)
\(\Leftrightarrow sinA-sinB+sinA.sinB\left(sinA-sinB\right)=0\)
\(\Leftrightarrow\left(sinA-sinB\right)\left(1+sinA.sinB\right)=0\)
\(\Leftrightarrow sinA=sinB\)
\(\Leftrightarrow A=B\)
Tam giác cân tại C
Đúng 0
Bình luận (0)
23 tháng 1 2021 lúc 15:34
Cho tam giác ABC có A(-1;0),B(4;0),C(0;m), m≠0. Gọi G là trọng tâm của tam giác ABC. Xác định m để tam giác GAB vuông tại G
23 tháng 1 2021 lúc 15:38
Cho tam giác ABC có A(1;-1),B(3;-3),C(6;0). Diện tích tam giác ABC là
#TK
Suy ra diện tích tam giác ABC là 1/2.AB.BC = 6.
Đúng 1
Bình luận (0)
23 tháng 1 2021 lúc 15:50
Tìm bán kính đường tròn đi qua ba điểm A(0;4),B(3;4),C(3;0)
Phương trình đường tròn (C) có dạng:
x2 + y2 -2ax – 2by + c= 0 ( a2+ b2 –c > 0)
Do 3 điểm A; B; C thuộc (C) nên
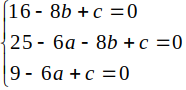
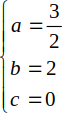
Vậy bán kính R= \(\sqrt{a^2+b^2-c^2}=\sqrt{\left(\dfrac{3}{2}\right)^2+2^2}=2.5\)
Đúng 0
Bình luận (0)
23 tháng 1 2021 lúc 16:02
Trong mp tọa độ Oxy cho tam giác ABC có A(1;0).B(-1;1),C(5;-1). Tọa độ trực tâm H của tam giác ABC là
Giả sử trực tâm của tam giác ABC có tọa độ \(H\left(x;y\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{BC}=\left(6;-2\right)\\\overrightarrow{AH}=\left(x-1;y\right)\end{matrix}\right.\Rightarrow\overrightarrow{BC}\perp\overrightarrow{AH}\Leftrightarrow\overrightarrow{AH}.\overrightarrow{BC}=0\)
\(\Leftrightarrow6\left(x-1\right)-2y=0\)
\(\Leftrightarrow3x-y=3\left(1\right)\)
Lại có:
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-2;1\right)\\\overrightarrow{CH}=\left(x-5;y+1\right)\end{matrix}\right.\Rightarrow\overrightarrow{AB}\perp\overrightarrow{CH}\Leftrightarrow\overrightarrow{CH}.\overrightarrow{AB}=0\)
\(\Leftrightarrow-2\left(x-5\right)+y+1=0\)
\(\Leftrightarrow-2x+y=-11\left(2\right)\)
\(\left(1\right);\left(2\right)\Rightarrow\left\{{}\begin{matrix}x=-8\\y=-27\end{matrix}\right.\Rightarrow H\left(-8;-27\right)\)
Đúng 3
Bình luận (1)