Phương trình đường tròn (C) có dạng:
x2 + y2 -2ax – 2by + c= 0 ( a2+ b2 –c > 0)
Do 3 điểm A; B; C thuộc (C) nên
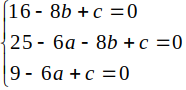
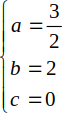
Vậy bán kính R= \(\sqrt{a^2+b^2-c^2}=\sqrt{\left(\dfrac{3}{2}\right)^2+2^2}=2.5\)
Phương trình đường tròn (C) có dạng:
x2 + y2 -2ax – 2by + c= 0 ( a2+ b2 –c > 0)
Do 3 điểm A; B; C thuộc (C) nên
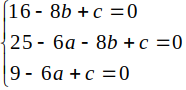
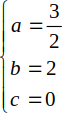
Vậy bán kính R= \(\sqrt{a^2+b^2-c^2}=\sqrt{\left(\dfrac{3}{2}\right)^2+2^2}=2.5\)
cho tam giác ABC
AC=3cm, BC=6cm, đường trung tuyến AM=4cm
a. tính BC? diện tích tam giác ABC
b. Tính đường cao AH?góc B? góc C
c. tính bán kính đường tròn ngoại tiếp
Trong mp Oxy cho 3 điểm A(-1;2) B(3;4) C(2;-2)
a. tính chu vi và S t/giác ABC
b. Tìm tọa độ D/ ABCD là hình thang cân có 2 đáy là AB,CD
c. Tìm tọa độ E nằm trên Ox cách đều A và C
d. Tìm tọa độ G,H,I lần lượt là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp t/g ABC
e. Tìm tọa độ M nằm trên tren Ox sao cho t/g MAB vuông tại M
Viết pt đg thẳng denta đi qua A(-2;0) và tạo với đg thẳng d : x +3y -3=0 một góc 45°
cho tam giác ABC vuông tại A , góc B = 75 độ . Tính
a) (\(\overrightarrow{BA},\overrightarrow{BC}\))
b) (\(\overrightarrow{CA},\overrightarrow{CB}\))
c) (\(\overrightarrow{AB},\overrightarrow{BC}\))
Trong mp Oxy cho A(1;4) B(-3;11) C(2;5) D(-4;3) E(2;-4)
a. Tìm tọa độ điểm M nằm trên Õ sao cho MA//CD
b. Tìm tọa độ điểm N1,N2 là hình chiếu của D trên các trục tọa độ
cho tam giác ABC đều và một điểm P nằm trong tam giác sao cho \(PB\ne PC\). Các đường thẳng PB và PC lần lượt cắt AC và AB tương ứng với tại D và E. Cho biết: PB:PC=AD:AE. Tìm góc BPC
Cho M là 1 điểm thuộc nửa đường tròn lượng giác sao cho xÔM = α, khoảng cách từ M đến 2 trục Ox và Oy bằng nhau, hỏi sin, cos của α là bao nhiêu?
giúp e với ạ
Cho tam giác AOB cân tại O có OA=a và các đường cao OH, AK. Giả sử góc AOH =\(\alpha\). Tính AK và OH theo a và \(\alpha\)