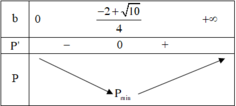
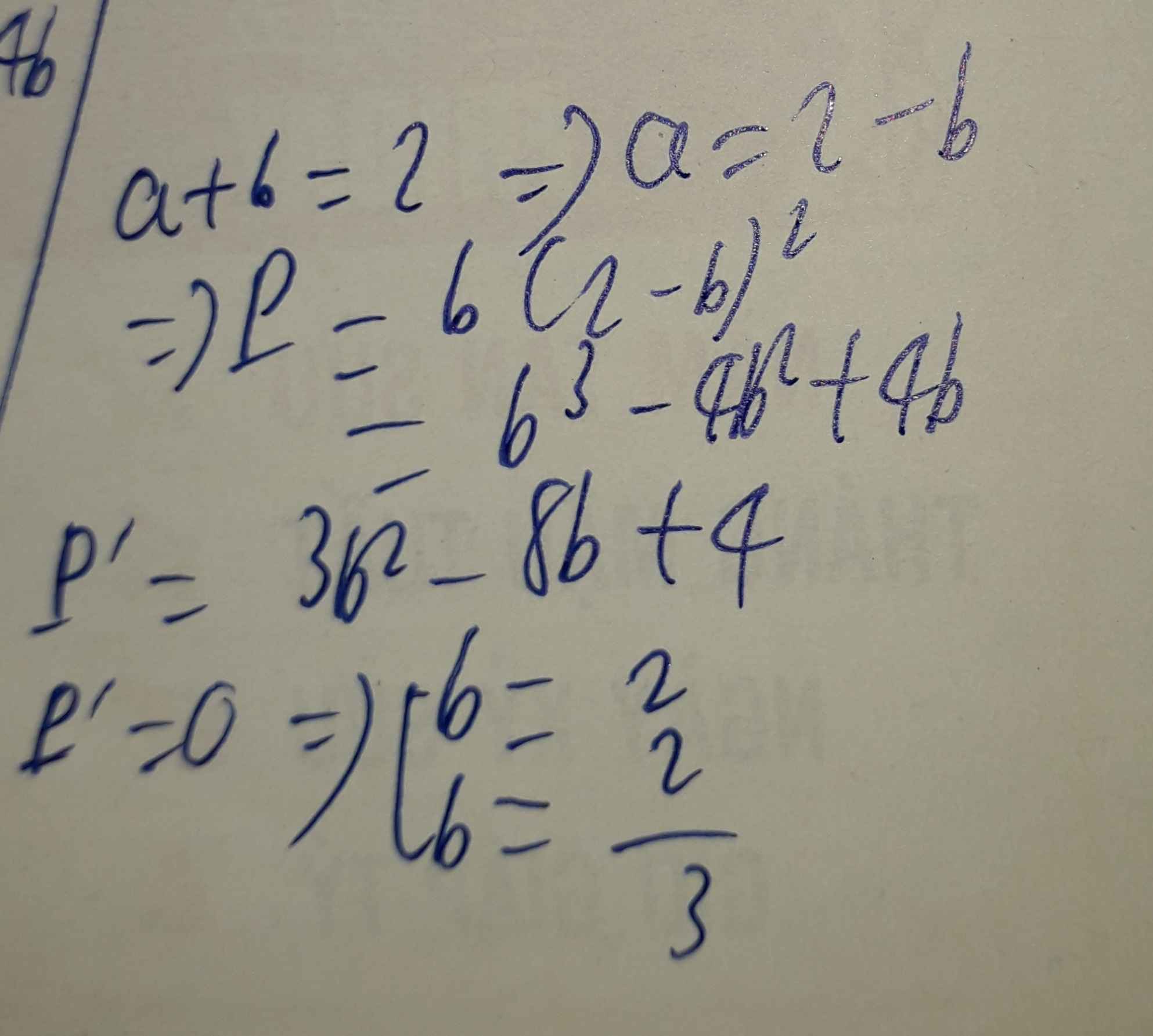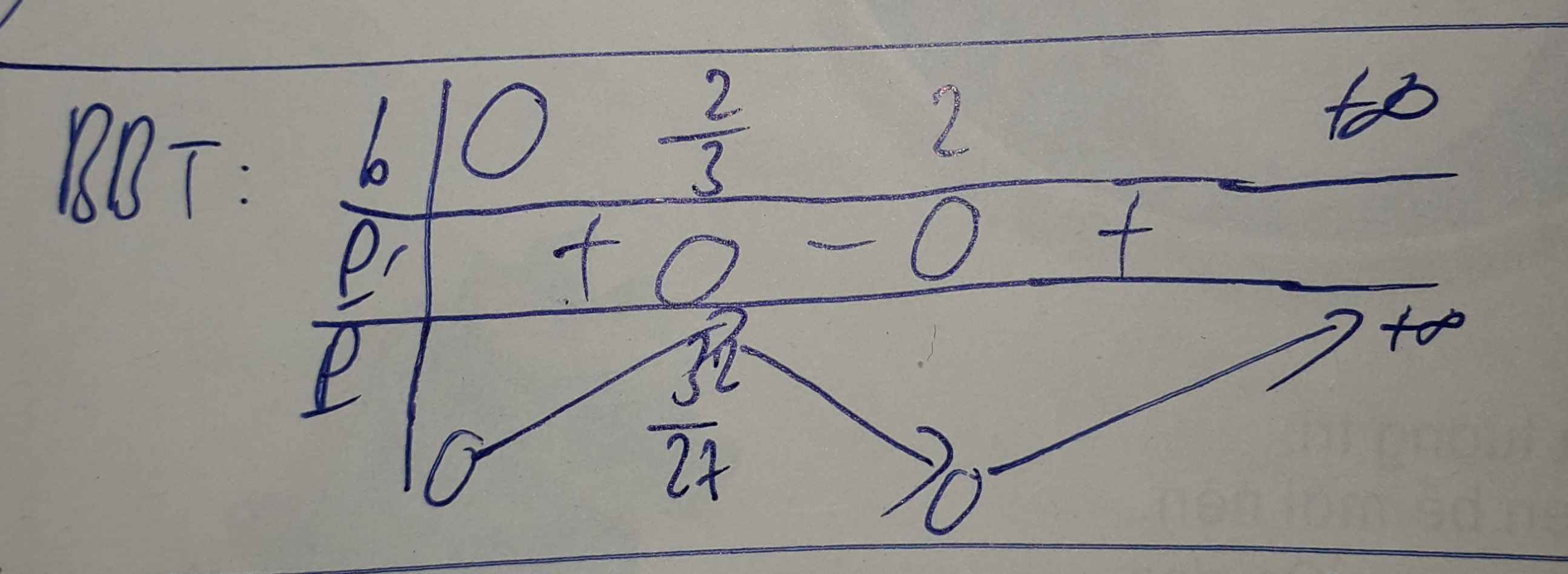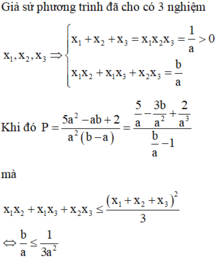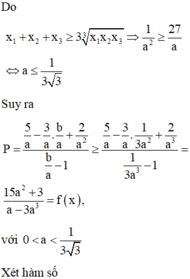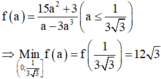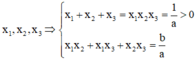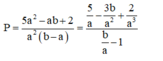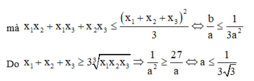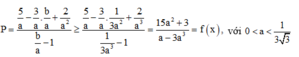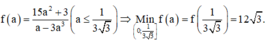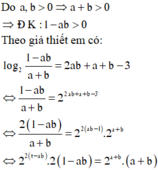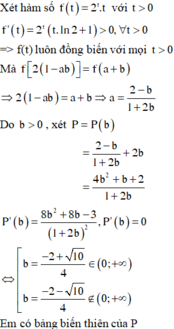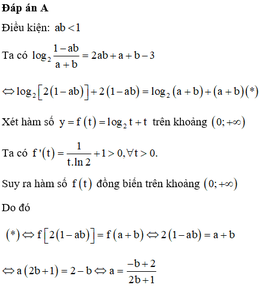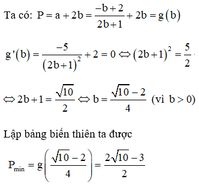Xét các số thực dương \(a;b\) thay đổi và thỏa mãn : \(a+b\ge2\). Tìm giá trị nhỏ nhất của biểu thức :
\(P=\sqrt{16a^2.b^2+9}.\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\).
P/s : Em xin phép đăng bài toán nhờ quý thầy cô giáo và các bạn giúp đỡ, em cám ơn nhiều lắm ạ!