Giúp em với ạ
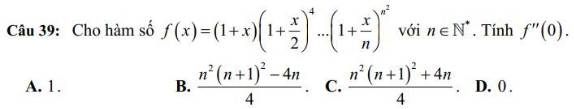
Giúp em với ạ
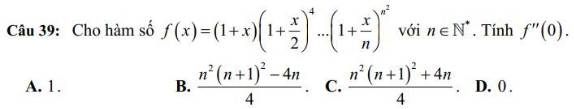
Bài này khuyên thực lòng là bạn nên sử dụng cách trắc nghiệm để giải, vì yêu cầu giải theo kiểu tự luận sẽ mất đến cả trang giấy.
Giúp em với ạ !!!!!!
Chọn và giải thích tại sao lại chọn đáp án đó ạ. Em cảm ơn ạ


46.
ĐKXĐ: \(x\ne\dfrac{2}{3}\)
\(y'=\dfrac{4x\left(3x-2\right)-3\left(2x^2-1\right)}{\left(3x-2\right)^2}=\dfrac{6x^2-8x+3}{\left(3x-2\right)^2}\)
\(y''\left(x\right)=\dfrac{\left(12x-8\right)\left(3x-2\right)^2-6\left(3x-2\right)\left(6x^2-8x+3\right)}{\left(3x-2\right)^4}\)
\(y''=0\Rightarrow\left(12x-8\right)\left(3x-2\right)^2-6\left(3x-2\right)\left(6x^2-8x+3\right)=0\)
\(\Leftrightarrow\left(3x-2\right)\left[\left(12x-8\right)\left(3x-2\right)-6\left(6x^2-8x+3\right)\right]=0\)
\(\Leftrightarrow-2\left(3x-2\right)=0\)
\(\Leftrightarrow x=\dfrac{2}{3}\left(ktm\right)\)
Vậy pt đã cho vô nghiệm
44.
\(f'\left(x\right)=-\dfrac{mx^3}{3}+\dfrac{mx^2}{2}-\left(3-m\right)x\)
\(f''\left(x\right)=-x^2+mx+m-3\)
\(f'\left(x\right)\le0;\forall x\)
\(\Leftrightarrow\Delta=m^2+4\left(m-3\right)\le0\)
\(\Leftrightarrow m^2+4m-12\le0\)
\(\Rightarrow-6\le m\le2\)
45.
\(f'\left(x\right)=3cos3x+3sin3x\)
\(f''\left(x\right)=-9sin3x+9cos3x\)
\(f''\left(x\right)+a.f'\left(x\right)+b.f\left(x\right)=0\)
\(\Leftrightarrow-9sin3x+9cos3x+a.\left[3cos3x+3sin3x\right]+b.\left[sin3x-cos3x\right]=0\)
\(\Leftrightarrow\left(3a+b-9\right)sin3x+\left(3a-b+9\right)cos3x=0\)
\(\Rightarrow\left\{{}\begin{matrix}3a+b-9=0\\3a-b+9=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=0\\b=9\end{matrix}\right.\)
Giúp em với ạ !!!!!!
Chọn và giải thích tại sao lại chọn đáp án đó ạ. Em cảm ơn ạ


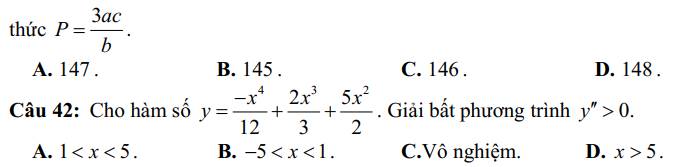
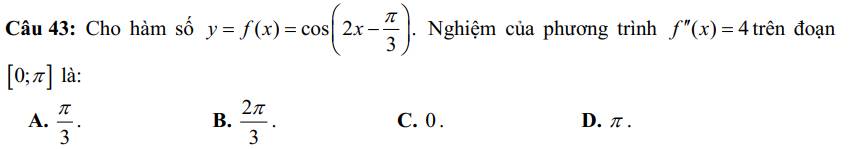
38.
\(f\left(x\right)=a_0+a_1x+a_2x^2+...+a_{60}x^{60}\)
\(\Rightarrow f'\left(x\right)=a_1+2a_2x+3a_3x^2+...+60a_{60}x^{59}\)
\(\Rightarrow f''\left(x\right)=2a_2+6a_3x+...+3540a_{60}x^{58}\)
Thay \(x=1\)
\(\Rightarrow f''\left(1\right)=2a_2+6a_3+12a_4+...+3540a_{60}\)
\(\Rightarrow T=2024a_0+f''\left(1\right)\)
\(a_0=f\left(0\right)=1\)
\(f'\left(x\right)=30\left(1-3x+2x^2\right)^{29}.\left(4x-3\right)\)
\(f''\left(x\right)=120\left(1-3x+2x^2\right)^{29}+30.29.\left(1-3x+2x^2\right).\left(4x-3\right)^2\)
\(\Rightarrow f''\left(1\right)=120.0+30.29.0.1=0\)
\(\Rightarrow T=2024.1+0=2024\)
41.
\(x^2.f'\left(x\right)-x.f\left(x\right)=-x^3.e^{x^2}+x.\left[f'\left(x\right)-f\left(x\right)\right]\)
\(\Leftrightarrow\left(x^2-x\right).f'\left(x\right)=-x^3.e^{x^2}\)
\(\Rightarrow f'\left(x\right)=\dfrac{-x^2.e^{x^2}}{x-1}\)
\(\Rightarrow f''\left(x\right)=\dfrac{-x^2+2x}{\left(x-1\right)^2}.e^{x^2}-\dfrac{2x^3}{x-1}.e^{x^2}\)
\(\Rightarrow f''\left(3\right)=-\dfrac{3}{4}.e^9-27e^9=\dfrac{-111}{4}e^9\)
\(\Rightarrow P=\dfrac{3.111.4}{9}=148\)
42.
\(y'=-\dfrac{1}{3}x^3+2x^2+5x\)
\(y''=-x^2+4x+5\)
\(-x^2+4x+5>0\Rightarrow-1< x< 5\)
Đáp án có gì đó sai sai (mặc dù chọn A chắc cũng được)
43.
\(f'\left(x\right)=-2sin\left(2x-\dfrac{\pi}{3}\right)\)
\(f''\left(x\right)=-4cos\left(2x-\dfrac{\pi}{3}\right)\)
\(f''\left(x\right)=4\Leftrightarrow cos\left(2x-\dfrac{\pi}{3}\right)=-1\)
\(\Leftrightarrow2x-\dfrac{\pi}{3}=\pi+k2\pi\)
\(\Leftrightarrow x=\dfrac{2\pi}{3}+k\pi\)
\(\Rightarrow x=\dfrac{2\pi}{3}\)
Giúp em với ạ !!!!!!
Chọn và giải thích tại sao lại chọn đáp án đó ạ. Em cảm ơn ạ


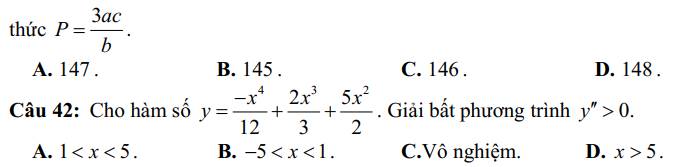
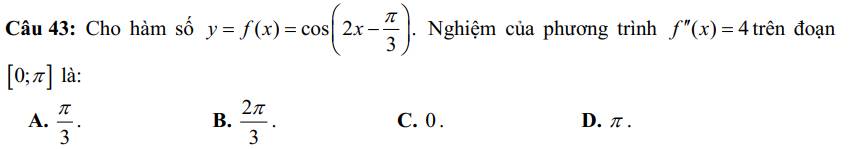

\(3log_a^2b-24log_b\left(a\sqrt[3]{b}\right)=-8\)
\(\Leftrightarrow3log_a^2b-24log_ba-8log_bb=-8\)
\(\Leftrightarrow3log_a^2b-\dfrac{24}{log_ab}=0\)
\(\Leftrightarrow log_a^3b=8\)
\(\Rightarrow log_ab=2\)
\(\Rightarrow P=log_aa+log_a\sqrt[3]{a}+log_a\sqrt[3]{b}=2017=1+\dfrac{1}{3}+\dfrac{1}{3}log_ab+2017\)
\(=\dfrac{4}{3}+\dfrac{2}{3}+2017=2019\)
Câu 72:
Ta có: \(T=log_{a^2}b-log_{\sqrt{b}}a^3\)
\(=\dfrac{1}{log_ba^2}-3log_{\sqrt{b}}a\)
\(=\dfrac{1}{2log_ba}-3\cdot\dfrac{1}{log_a\sqrt{b}}\)
\(=\dfrac{1}{2}\cdot\dfrac{1}{log_ba}-3\cdot\dfrac{1}{\dfrac{1}{2}log_ab}\)
\(=\dfrac{1}{2}\cdot log_ab-3\cdot\dfrac{1}{\dfrac{1}{2}log_ab}\)
\(=\dfrac{1}{2}\cdot m-3\cdot\dfrac{1}{\dfrac{1}{2}m}\)
\(=\dfrac{m^2-12}{2m}\)
⇒ Chọn B
\(T=log_{a^2}\dfrac{a^4\sqrt[3]{b}}{c^3}\)
\(=\dfrac{1}{2}\cdot log_a\left(a^4\cdot\dfrac{b^{\dfrac{1}{3}}}{c^3}\right)\)
\(=\dfrac{1}{2}\left(log_aa^4+log_ab^{\dfrac{1}{3}}-log_ac^3\right)\)
\(=\dfrac{1}{2}\left(4+\dfrac{1}{3}\cdot log_ab-3\cdot log_ac\right)\)
\(=\dfrac{1}{2}\left(4+\dfrac{1}{3}\cdot6-\dfrac{3}{3}\right)=\dfrac{1}{2}\left(4+2-1\right)=\dfrac{1}{2}\cdot5=\dfrac{5}{2}\)
=>Chọn A
\(P=log_{\sqrt{a}}\left(\dfrac{b}{c}\right)=log_{a^{\dfrac{1}{2}}}\left(\dfrac{b}{c}\right)\)
\(=2\cdot log_a\left(\dfrac{b}{c}\right)\)
\(=2\cdot\left(log_ab-log_ac\right)\)
\(=2\cdot\left(log_ab-\dfrac{log_bc}{log_ba}\right)\)
\(=2\left(log_ab-log_bc\cdot log_ab\right)=2\left(7-5\cdot7\right)=2\left(7-35\right)=-56\)
=>Chọn B
\(log_{ab^2}x^2=\dfrac{1}{log_{x^2}ab^2}=\dfrac{1}{\dfrac{1}{2}\cdot log_xab^2}\)
\(=\dfrac{1}{\dfrac{1}{2}\cdot\left(log_xa+log_xb^2\right)}\)
\(=\dfrac{2}{log_xa+2\cdot log_xb}=\dfrac{2}{\dfrac{1}{log_ax}+\dfrac{2}{log_bx}}\)
\(=\dfrac{2}{\dfrac{1}{a}+\dfrac{2}{b}}=2:\dfrac{b+2a}{ab}=\dfrac{2ab}{2a+b}\)
=>Chọn D

\(X=\dfrac{\sqrt[3]{m}}{m^2\cdot\sqrt[5]{m}}=\dfrac{m^{\dfrac{1}{3}}}{m^2\cdot m^{\dfrac{1}{5}}}=\dfrac{m^{\dfrac{1}{3}}}{m^{\dfrac{11}{5}}}=m^{\dfrac{1}{3}-\dfrac{11}{5}}=m^{-\dfrac{28}{15}}\)
\(a=\dfrac{1}{\sqrt[3]{m^2}}=\dfrac{1}{m^{\dfrac{2}{3}}}=m^{-\dfrac{2}{3}}\)
\(a^{\dfrac{14}{5}}=\left(m^{-\dfrac{2}{3}}\right)^{\dfrac{14}{5}}=m^{-\dfrac{2}{3}\cdot\dfrac{14}{5}}=m^{-\dfrac{28}{15}}=X\)
=>Chọn D