Cho tam giác ABC vuông tại A. Vẽ AH vuông BC( H thuộc BC). Cho biết BAH < CAH. Hãy so sánh:
a. B và C
b. HB với HC
Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
a: \(\widehat{BAH}< \widehat{CAH}\)
nên \(90^0-\widehat{BAH}>90^0-\widehat{CAH}\)
hay \(\widehat{B}>\widehat{C}\)
b: Vì \(\widehat{B}>\widehat{C}\)
nên AB<AC
=>HB<HC
Đúng 4
Bình luận (0)
Kẻ AH vuông góc BC tại H.
Trên tia AH lấy A' sao cho AH=HA'
Gọi M' là giao của (d) với A'B
MA+MB>=AM'+MB
mà AM'=A'M'
nên MA+MB>=MA'+MB=A'B
Dấu = xảy ra khi M trùng với M'
Đúng 0
Bình luận (0)
1:
a: P=6x^2-5x+1-6x^2-2x-7=-7x-6
b: P(2)=-14-6=-20
c: P(x)=0
=>-7x-6=0
=>7x+6=0
=>x=-6/7
Đúng 0
Bình luận (0)
Giúp mình bài này với 😭
a: Xét ΔADB vuông tại D và ΔADC vuông tại D có
AB=AC
AD chung
=>ΔADB=ΔADC
=>DB=DC
c: Xét ΔABC có
D là trung điểm của BC
DK//AB
=>K là trung điểm của AC
ΔADC vuông tại D có DK là trung tuyến
nên DK=KC
=>ΔKDC cân tại K
Đúng 0
Bình luận (0)
cho tam giác abc có góc c < góc b < 90 độ. kẻ ah vuông bc ( h thuộc bc ) gọi m là 1 điểm nằm giữa h và b , n là 1 điểm trên đường thẳng bc nhưng không thuộc đoạn bcchứng minh rằnga) hb vuông hcb) am < ab < an
Xem chi tiết
cho tam giác ABC vuông cân tại A. qua A kẻ đường thẳng D sao cho BvàC cùng thuộc nửa mặt phẳng bờ là đường thẳng D. gọi I là trung điểm của BC. gọi H,M,K lần lượt là hình chiếu của B,I,C lên đường thẳng C
a, C/m tam giác BHA=tam giác AKC
b,C/m tam giác HIA=tam giác KIC
c, Đường thẳng D ở vị trí nào để diện tích tứ giác BCKH lớn nhất
a: Xét ΔAHB và ΔCKA có
góc AHB=góc AKC=90 độ
AB=CA
góc HAB=góc ACK
=>ΔAHB=ΔCKA
b: ΔAHB=ΔCKA
=>AH=CK
Xet ΔHIA và ΔKIC có
IA=IC
AH=CK
góc HAI=góc ICK
=>ΔHIA=ΔKIC
=>IH=IK
c: \(S_{BCKH}=\dfrac{1}{2}\cdot\left(BH+CK\right)\cdot HK\)
\(=\dfrac{1}{2}\cdot HK^2=IM^2< =IA^2\)
Dấu = xảy ra khi M trùng với A
=>d vuông góc AI
Đúng 1
Bình luận (0)
Cho ΔABC cân tại A, M là trung điểm của AC, gọi E và F là chân các đường vuông góc kẻ từ A và C đến đường thẳng BM
Xem chi tiết
a) EM = FM
b) So sánh AB và AE+BF/2
a: Xét ΔEMA vuông tại E và ΔFMC vuông tại F có
MA=MC
\(\widehat{AME}=\widehat{CMF}\)(hai góc đối đỉnh)
Do đó: ΔEMA=ΔFMC
=>EM=FM
Đúng 1
Bình luận (0)
cho tam giác def vuông tại d , trên canh de lấy m sao cho m khác d và e , trên cạnh df lấy n sao cho n khác d và f , cm rằng nm < fe
Xét ΔDNM có \(\widehat{FNM}\) là góc ngoài tại đỉnh N
nên \(\widehat{FNM}=\widehat{NDM}+\widehat{NMD}=90^0+\widehat{NMD}>90^0\)
Xét ΔFNM có \(\widehat{FNM}\) là góc tù
nên FM là cạnh lớn nhất trong ΔFNM
=>FM>NM
Xét ΔDFM có \(\widehat{FME}\) là góc ngoài tại đỉnh M
nên \(\widehat{FME}=\widehat{MFD}+\widehat{MDF}=90^0+\widehat{MFD}>90^0\)
Xét ΔFME có \(\widehat{FME}>90^0\)
nên FE là cạnh lớn nhất trongΔFME
=>FE>FM
mà FM>NM
nên FE>NM
=>NM<FE
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A , góc C=30’ .CM:BC=2AB
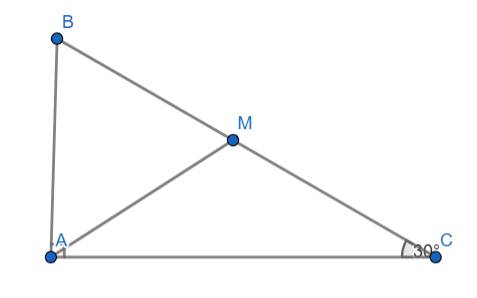
Gọi M là trung điểm của BC
⇒ AM là đường trung tuyến của BC
Và ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{B}=180^o-90^o-30^o=60^o\)
Mà: \(AM=\dfrac{1}{2}BC\Rightarrow AM=BM\)
\(\Rightarrow\Delta ABM\) là tam giác cân
Lại có \(\widehat{B}=60^o\) khi trong tam giác cân có 1 góc bằng 60 độ thì tam giá đó là tam giác đều
\(\Rightarrow AM=BM=AB\)
\(\Rightarrow AB=AM=\dfrac{1}{2}BC\left(dpcm\right)\)
Đúng 2
Bình luận (0)
Giúp mình nhanh với mình đang gấp lắm rồi
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a.Đường phân giác bd(d thuộc ac).từ d kẻ dh vuông góc với bc tại h.Đường thẳng dh cắt đường thẳng ab tại k a)chứng minh ad=hd b)so sánh độ dài ad và dc c)chứng minh bd vuông góc với kc
a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
góc ABD=góc HBD
=>ΔBAD=ΔBHD
=>DA=DH
b: AD=DH
DH<DC
=>AD<DC
c: Xét ΔBKC có
KH,CA là đường cao
KH cắt CA tại D
=>D là trực tâm
=>BD vuông góc KC
Đúng 0
Bình luận (0)