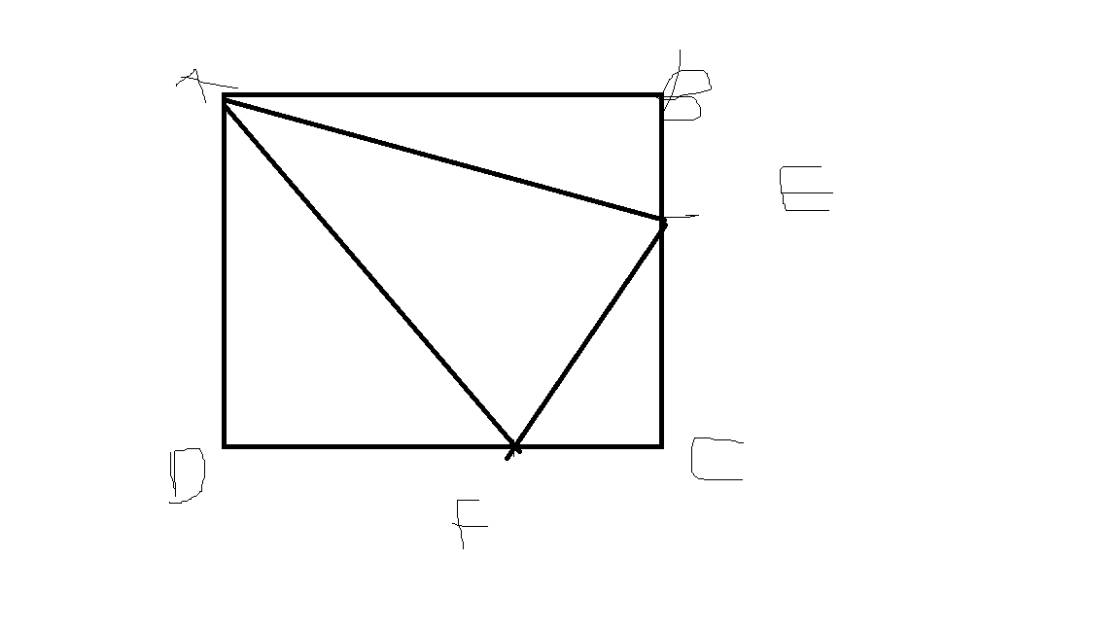
Câu 4: Cho hình vuông ABCD, M thuộc đường chéo AC. Gọi E,F theo thứ tự là hình chiếu của M trên AD, CD. Chứng minh rằng:
a. BM vuông góc EF
b. Các đường thẳng BM, EF, CE đồng quy.
Bài 12: Hình vuông
Một mảnh đất hình vuông có độ dài hai cạnh là a và b. Hãy tính diện tích của mảnh đất nói trên.
Cho hình thoi ABCD có góc ABC = 60 độ. Kẻ AE vuông góc với DC (E thuộc DC), AF vuông góc với BC(F thuộc BC).
a) Cm tam giác AEF đều.
b) Cm FE song song với BD.
(Mình đang cần gấp mong các bạn giúp mình)
a:
ABCD là hình thoi
=>\(\widehat{C}+\widehat{B}=180^0\) và \(\widehat{B}=\widehat{D}=60^0\)
=>\(\widehat{C}=180^0-60^0=120^0\)
Xét ΔAFB vuông tại F và ΔAED vuông tại E có
AB=AD
\(\widehat{B}=\widehat{D}\)
Do đó: ΔAFB=ΔAED
=>AF=AE và BF=ED
Xét tứ giác AECF có
\(\widehat{AEC}+\widehat{AFC}+\widehat{C}+\widehat{FAE}=360^0\)
=>\(\widehat{FAE}+120^0+90^0+90^0=360^0\)
=>\(\widehat{FAE}=60^0\)
Xét ΔAEF có AE=AF và \(\widehat{FAE}=60^0\)
nên ΔAEF đều
b: CE+ED=CD
CF+FB=CB
mà CD=CB và ED=FB
nên CE=CF
Xét ΔCBF có \(\dfrac{CE}{CD}=\dfrac{CF}{CB}\)
nên EF//BD
Đúng 0
Bình luận (1)
Cho tam giác ABC vuông tại A. Đường cao AH.kẻ HD vuông góc với AB tại D ,kẻ HE vuông góc với AC tại E a, C/m tứ giác ADHE là hình chữ nhật b, C/m AH=DE ? c, tam giác ABC cần có điều kiện gì thì tứ giác ADHE là hình vuông Viết GT, KL
a: Xét tứ giác ADHE có
góc ADH=góc AEH=góc DAE=90 độ
nên ADHE là hình chữ nhật
b: Vì ADHE là hình chữ nhật
nên AH=DE
c: Để ADHE là hình vuông thì AH là phân giác của góc DAE
mà AH vuông góc vơi BC
nên ΔABC cân tại A
=>AB=AC
Đúng 1
Bình luận (0)
Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của AB, BD. DC, CA. Tìm điều kiện của tứ giác ABCD để EFGH là hình vuông.
Xét ΔABC có
E,H lần lượt là trung điểm của AB,AC
=>EH là đường trung bình của ΔABC
=>EH//BC và EH=BC/2
Xét ΔBDC có
F,G lần lượt là trung điểm của DB,DC
=>FG là đường trung bình của ΔBDC
=>FG//BC và FG=BC/2
EH//BC
FG//BC
Do đó: EH//FG
EH=BC/2
FG=BC/2
Do đó: EH=FG
Xét tứ giác EHGF có
EH//FG
EH=FG
Do đó: EHGF là hình bình hành
Xét ΔBAD có
E,F lần lượt là trung điểm của BA,BD
=>EF là đường trung bình
=>EF//AD và EF=AD/2
Để EHGF là hình vuông thì EH=EF và EH\(\perp\)EF
EH=EF
EH=BC/2
EF=AD/2
Do đó: BC=AD
EH\(\perp\)EF
EH//BC
Do đó: EF\(\perp\)BC
EF\(\perp\)BC
EF//AD
Do đó: BC\(\perp\)AD
Vậy: Khi BC=AD và BC\(\perp\)AD thì EFGH là hình vuông
Đúng 1
Bình luận (0)
cho hình vuông ABCD. Từ điểm M thuộc cạnh BC vẽ đường thẳng cắt CD tại K
sao cho AMB=AMK. kẻ AH vuông góc với MK ở
c/m tam giac ABM=AHM va AH=HD
b, c/m tam giac DAK= tam giac AHK
c, c/m MAK=1/2 A= 45 do
a: Xét ΔAHM vuông tại H và ΔABM vuông tại B có
MA chung
\(\widehat{AMH}=\widehat{BMA}\)
Do đó: ΔAHM=ΔABM
=>AH=AB=AD
b: Xét ΔADK vuông tại D và ΔAHK vuông tại H có
AK chung
AD=AH
Do đó: ΔADK=ΔAHK
c: \(\widehat{MAK}=\widehat{MAH}+\widehat{KAH}\)
\(=\dfrac{1}{2}\left(\widehat{BAH}+\widehat{DAH}\right)=\dfrac{1}{2}\cdot90^0=45^0\)
Đúng 0
Bình luận (1)
Cho hình bình hành ABCD. Vẽ về phía ngoài hình bình hành hai hình vuông ABEF và ADGH. Chứng minh:a) AC FH.b) AC vuông góc FH.c) CEG là tam giác vuông cân.
Đọc tiếp
Cho hình bình hành ABCD. Vẽ về phía ngoài hình bình hành hai hình vuông ABEF và ADGH. Chứng minh:
a) AC = FH.
b) AC vuông góc FH.
c) CEG là tam giác vuông cân.
Cho hình vuông ABCD . Trên cạnh BC lấy điểm E , trên tia đối của tia DC lấy điểm F sao cho BE = DF .
a) Chứng minh ΔAEH vuông cân tại A
b) Gọi H là điểm đối xứng của A qua EF . Chứng minh AEHF là hình vuông.
a: Sửa đề: ΔAEF vuông cân tại A
Xét ΔADF vuông tại D và ΔABE vuông tại B có
AD=AB
DF=BE
Do đó: ΔADF=ΔABE
=>AF=AE và \(\widehat{DAF}=\widehat{BAE}\)
mà \(\widehat{BAE}+\widehat{DAE}=90^0\)
nên \(\widehat{DAF}+\widehat{DAE}=90^0\)
=>\(\widehat{FAE}=90^0\)
Xét ΔAEF có \(\widehat{FAE}=90^0\) và AE=AF
nên ΔAEF vuông cân tại A
b: Gọi giao điểm của AH với EF là M
H đối xứng A qua EF
=>EF là đường trung trực của HA
=>EH=EA và FH=FA
mà AH=AE
nên EH=EA=FH=FA
Xét tứ giác AEHF có
AE=HE=HF=FA
nên AEHF là hình thoi
Hình thoi AEHF có \(\widehat{FAE}=90^0\)
nên AEHF là hình vuông
Đúng 2
Bình luận (0)
Cho ▲ABC vuông cân tại A. Trên BC lấy M,N sao cho BM=CN< . MQ vuông góc BC, NP vuông góc BC ( Q ϵ AB, P ϵ AC).
a) Tứ giác MNPQ là hình gì?
b) Xác định vị trí của M và N để MNPQ là hình vuông.
a: \(NP\perp BC;MQ\perp BC\)
Do đó: NP//MQ
ΔMQB vuông tại M có \(\widehat{B}=45^0\)
nên ΔMQB vuông cân tại M
=>MQ=MB
ΔNPC vuông tại N có \(\widehat{C}=45^0\)
nên ΔNPC vuông cân tại N
=>NP=NC
NP=NC
MQ=MB
NC=MB
Do đó: NP=MQ
Xét tứ giác MNPQ có
NP//MQ
NP=MQ
Do đó: MNPQ là hình bình hành
mà \(\widehat{PNM}=90^0\)
nên MNPQ là hình chữ nhật
b: Để MNPQ là hình vuông thì QM=MN
=>MB=MN
=>\(MB=MN=NC\)
=>\(MN=\dfrac{BC}{3}\)
Vậy: M,N nằm trên đoạn BC sao cho \(CN=NM=MB=\dfrac{CB}{3}\) thì MNPQ là hình vuông
Đúng 2
Bình luận (0)
Giúp mình với ạ :)
Cho hình vuông ABCD hãy dựng điểm E thuộc cạnh BC điểm F thuộc cạnh CD sao cho tam giác AEF là tam giác đều.