Một nguyên hàm của hàm số f(x) = sin2x là:
A. F(x) = 2cos2x. B. F(x) = −cos2x.
C. \(F\left(x\right)=\dfrac{1}{2}\cos2x\). D. \(F\left(x\right)=\dfrac{-1}{2}\cos2x\).
Một nguyên hàm của hàm số f(x) = sin2x là:
A. F(x) = 2cos2x. B. F(x) = −cos2x.
C. \(F\left(x\right)=\dfrac{1}{2}\cos2x\). D. \(F\left(x\right)=\dfrac{-1}{2}\cos2x\).
Họ tất cả các nguyên hàm của hàm số 2ex là
A. 2xex + C. B. −2ex + C. C. 2ex. D. 2ex + C.
Thảo luận (1)Hướng dẫn giải
Nguyên hàm F(x) của hàm số f(x) = ex – 3e−x thỏa mãn F(0) = 4 là
A. F(x) = ex – 3e−x. B. F(x) = ex + 3e−2x.
C. F(x) = ex + 3e−x. D. F(x) = ex + 3e−x + 4.
Thảo luận (1)Hướng dẫn giảiTa có: \(F\left( x \right) = \int {\left( {{e^x} - 3{e^{ - x}}} \right)dx} = \int {{e^x}dx} - 3\int {{{\left( {\frac{1}{e}} \right)}^x}} dx = {e^x} + 3{e^{ - x}} + C\)
Lại có: \(F\left( 0 \right) = 4\) nên \({e^0} + 3{e^0} + C = 4\) nên \(C = 0\). Vậy \(F\left( x \right) = {e^x} + 3{e^{ - x}}\)
Chọn C
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hàm số f(x) có đạo hàm f'(x) liên tục trên ℝ, f(1) = 16 và \(\int\limits^3_1f'\left(x\right)=4\). Khi đó giá trị của f(3) bằng
A. 20. B. 16. C. 12. D. 10.
Thảo luận (1)Hướng dẫn giảiVì \(\int\limits_1^3 {f'\left( x \right)dx} = 4\) nên \(f\left( 3 \right) - f\left( 1 \right) = 4\), suy ra: \(f\left( 3 \right) = 4 + f\left( 1 \right) = 4 + 16 = 20\)
Chọn A
(Trả lời bởi Nguyễn Quốc Đạt)
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x2 – 2x, y = −x2 + 4x và hai đường thẳng x = 0, x = 3 là
A. −9. B. 9. C. \(\dfrac{16}{3}\). D. \(\dfrac{20}{3}\).
Thảo luận (1)Hướng dẫn giảiDiện tích hình phẳng cần tính là:
\(\int\limits_0^3 {\left| {{x^2} - 2x + {x^2} - 4x} \right|dx} = \int\limits_0^3 {\left| {2{x^2} - 6x} \right|dx} = \int\limits_0^3 {\left( { - 2{x^2} + 6x} \right)dx = \left( { - \frac{{2{x^3}}}{3} + 3{x^2}} \right)} \left| \begin{array}{l}3\\0\end{array} \right.\)
\( = - \frac{{{{2.3}^3}}}{3} + {3.3^2} = 9\)
Chọn B
(Trả lời bởi Nguyễn Quốc Đạt)
Cho đồ thị hàm số y = f(x) trên đoạn [−2;2] như Hình 4.32.
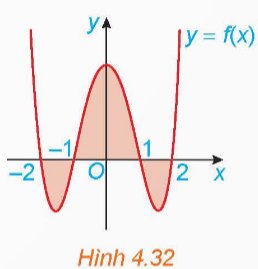
Biết \(\int\limits^{-1}_{-2}f\left(x\right)dx=\int\limits^2_1f\left(x\right)dx=\dfrac{-22}{15}\) và \(\int\limits^1_{-1}f\left(x\right)dx=\dfrac{76}{15}\). Khi đó, diện tích của hình phẳng được tô màu là:
A. 8. B. \(\dfrac{22}{15}\). C. \(\dfrac{32}{15}\). D. \(\dfrac{76}{15}\).
Thảo luận (1)Hướng dẫn giảiDiện tích phần được tô màu là: \( - \int\limits_{ - 2}^{ - 1} {f\left( x \right)dx} - \int\limits_1^2 {f\left( x \right)dx} + \int\limits_{ - 1}^1 {f\left( x \right)dx} = \frac{{22}}{{15}} + \frac{{22}}{{15}} + \frac{{76}}{{15}} = 8\)
Chọn A
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hình phẳng (S) giới hạn bởi đồ thị hàm số \(y=\sqrt{1-x^2}\), trục hoành và hai đường thẳng x = −1, x = 1. Thể tích của khối tròn xoay khi quay (S) quanh trục Ox là
A. \(\dfrac{3\pi}{4}\). B. \(\dfrac{3\pi}{2}\). C. \(\dfrac{2\pi}{3}\). D. \(\dfrac{4\pi}{3}\).
Thảo luận (1)Hướng dẫn giảiThể tích khối tròn xoay giới hạn bởi đồ thị hàm số \(y = \sqrt {1 - {x^2}} \), trục hoành và hai đường thẳng \(x = - 1,x = 1\)là:
.\(V = \pi \int\limits_{ - 1}^1 {\left( {1 - {x^2}} \right)dx = \pi \left( {x - \frac{{{x^3}}}{3}} \right)\left| \begin{array}{l}1\\ - 1\end{array} \right.} = \pi \left( {1 - \frac{1}{3} - \left( { - 1} \right) + \frac{{ - 1}}{3}} \right) = \frac{{4\pi }}{3}\).
Chọn D
(Trả lời bởi Nguyễn Quốc Đạt)
Một vật chuyển động có gia tốc là a(t) = 3t2 + t (m/s2). Biết rằng vận tốc ban đầu của vật là 2 m/s. Vận tốc của vật đó sau 2 giây là
A. 8 m/s. B. 10 m/s. C. 12 m/s. D. 16 m/s.
Thảo luận (1)Hướng dẫn giảiTa có: \(v\left( t \right) = \int {a\left( t \right)dt} = \int {\left( {3{t^2} + t} \right)dt} = {t^3} + \frac{{{t^2}}}{2} + C\)
Vì vận tốc ban đầu của vật là 2m/s nên: \({0^3} + \frac{{{0^2}}}{2} + C = 2\), do đó, \(C = 2\)
Suy ra: \(v\left( t \right) = {t^3} + \frac{{{t^2}}}{2} + 2\).
Vận tốc của vật đó sau 2 giây là: \(v\left( 2 \right) = {2^3} + \frac{{{2^2}}}{2} + 2 = 12\left( {m/s} \right)\)
Chọn C
(Trả lời bởi Nguyễn Quốc Đạt)
Tìm họ tất cả các nguyên hàm của các hàm số sau:
a) \(y=2^x-\dfrac{1}{x};\) b) \(y=x\sqrt{x}+3\cos x-\dfrac{2}{\sin^2x}\).
Thảo luận (1)Hướng dẫn giảia) \(\int {\left( {{2^x} - \frac{1}{x}} \right)dx} = \int {{2^x}dx} - \int {\frac{1}{x}dx} = \frac{{{2^x}}}{{\ln 2}} - \ln \left| x \right| + C\)
b) \(\int {\left( {x\sqrt x + 3\cos x - \frac{2}{{{{\sin }^2}x}}} \right)dx} = \int {{x^{\frac{3}{2}}}dx} + 3\int {\cos x - 2\int {\frac{{dx}}{{{{\sin }^2}x}}} } \)
\( = \frac{{2{x^2}\sqrt x }}{5} + 3\sin x + 2\cot x + C\)
(Trả lời bởi Nguyễn Quốc Đạt)
Tìm một nguyên hàm F(x) của hàm số \(f\left(x\right)=2\cos x+\dfrac{1}{\sin^2x}\) thỏa mãn điều kiện \(F\left(\dfrac{\pi}{4}\right)=-1\)..
Thảo luận (1)Hướng dẫn giảiTa có: \(\int {\left( {2\cos x + \frac{1}{{{{\sin }^2}x}}} \right)dx} = 2\int {\cos x + \int {\frac{{dx}}{{{{\sin }^2}x}} = 2\sin x - \cot x + C} } \)
Vì \(F\left( {\frac{\pi }{4}} \right) = - 1\) nên \(2\sin \frac{\pi }{4} - \cot \frac{\pi }{4} + C = - 1\), suy ra \(C = - \sqrt 2 \)
Do đó, \(F\left( x \right) = 2\sin x - \cot x - \sqrt 2 \).
(Trả lời bởi Nguyễn Quốc Đạt)