Cho tam giác vuông ABC có hai cạnh góc vuông AB=3cm,AC=4cm (H.9.31). Hãy đo độ dài cạnh BC và so sánh hai đại lượng \(A{B^2} + A{C^2}\) với \(B{C^2}\)
Bài 35. Định lí Pythagore và ứng dụng
Hoạt động 1 (SGK Kết nối tri thức với cuộc sống - Trang 93)
Thảo luận (1)
Hoạt động 2 (SGK Kết nối tri thức với cuộc sống - Trang 93)
Lấy giấy trắng cắt bốn tam giác vuông bằng nhau. Gọi a, b là độ dài hai cạnh góc vuông, c là độ dài cạnh huyền của các tam giác vuông này. Cắt một hình vuông bằng tấm bìa có cạnh dài a+b. Dán bốn tam giác vuông lên tấm bìa như Hình 9.32- Dùng ê ke kiểm tra phần bìa không bị che lấp có phải là hình vuông cạnh bằng c không. Từ đó tính diện tích phần bìa này theo c- Tổng diện tích bốn tam giác vuông có độ dài hai cạnh góc vuông a, b là bao nhiêu?- Diện tịch cả tấm bìa hình vuông cạnh a+ b bằng bao...
Đọc tiếp
Lấy giấy trắng cắt bốn tam giác vuông bằng nhau. Gọi a, b là độ dài hai cạnh góc vuông, c là độ dài cạnh huyền của các tam giác vuông này. Cắt một hình vuông bằng tấm bìa có cạnh dài a+b. Dán bốn tam giác vuông lên tấm bìa như Hình 9.32
- Dùng ê ke kiểm tra phần bìa không bị che lấp có phải là hình vuông cạnh bằng c không. Từ đó tính diện tích phần bìa này theo c
- Tổng diện tích bốn tam giác vuông có độ dài hai cạnh góc vuông a, b là bao nhiêu?
- Diện tịch cả tấm bìa hình vuông cạnh a+ b bằng bao nhiêu?
- So sánh \({c^2} + 2{\rm{a}}b\) với \({\left( {a + b} \right)^2}\)để rút ra nhận xét về mối quan hệ giữa hai đại lượng \({c^2}\) và \({a^2} + {b^2}\).
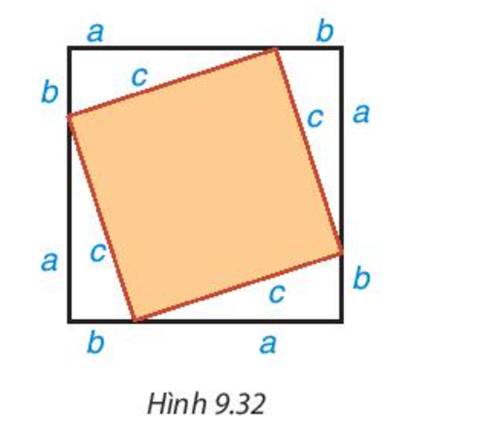
Thảo luận (2)Hướng dẫn giảiPhần bìa bị che lấp là hình vuông cạnh c. Diện tích của hình vuông là: \({c^2}\)
- Diện tích tấm bìa hình vuông là: \({\left( {a + b} \right)^2}\)
=> Diện tích bốn tam giác vuông là: \({\left( {a + b} \right)^2} - {c^2}\)
(Trả lời bởi Hà Quang Minh)
Câu hỏi (SGK Kết nối tri thức với cuộc sống - Trang 94)
Tìm độ dài x, y trong hình 9.35
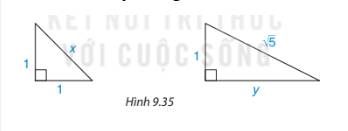
Thảo luận (2)Hướng dẫn giải\(x^2=1^2+1^2\left(pythagore\right)\\ \Rightarrow x=\sqrt{2}\\ \sqrt{5}^2=1^2+y^2\left(pythagore\right)\\ \Rightarrow y=\sqrt{4}=2\)
(Trả lời bởi 乇尺尺のレ)
Luyện tập 1 (SGK Kết nối tri thức với cuộc sống - Trang 94)
Trên giấy kẻ ô vuông (cạnh ô vuông bằng 1 cm), cho các điểm A, B, C như Hình 9.35. Tính độ dài các cạnh của tam giác ABC.
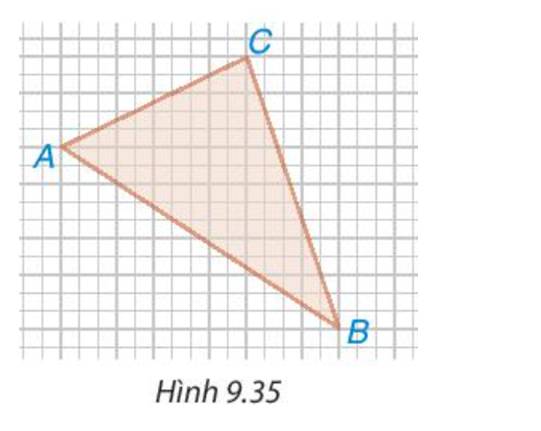
Thảo luận (1)Hướng dẫn giải\(AC^2=100+25=125\Rightarrow AC=5\sqrt[]{5}\left(cm\right)\)
\(AB^2=100+225=325\Rightarrow AB=5\sqrt[]{13}\left(cm\right)\)
\(BC^2=225+25=250\Rightarrow BC=5\sqrt[]{10}\left(cm\right)\)
(Trả lời bởi Nguyễn Đức Trí)
Vận dụng 1 (SGK Kết nối tri thức với cuộc sống - Trang 95)
Trở lại tình huống mở đầu. xem thành cầu thang như cạnh huyền BC của tam giác vuông ABC (hình 9.37). Tù đó, hãy tính độ dài cạnh BC để suy ra chiều dài cầu thang cần xây.
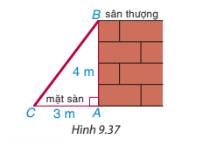
Thảo luận (1)Hướng dẫn giải\(BC^2=AB^2+AC^2\left(Pitago\right)\)
\(BC^2=16+9=25\)
\(\Rightarrow BC=5\left(m\right)\)
Vậy chiều dài cầu thang cần xây là 5m
(Trả lời bởi Nguyễn Đức Trí)
Luyện tập 2 (SGK Kết nối tri thức với cuộc sống - Trang 95)
Cho tam giác vuông với kích thước như Hình 9.37. Hãy tính độ dài x và cho biết những tam giác nào đồng dạng, viết đúng kí hiệu đồng dạng
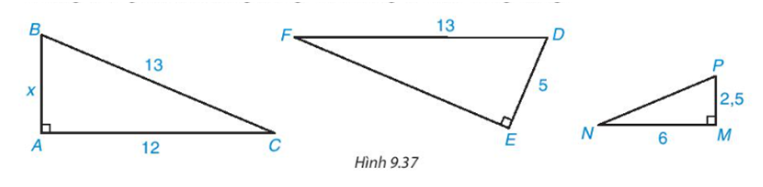
Thảo luận (1)Hướng dẫn giảiNhững tam giác đồng dạng là
- Tam giác ABC đồng dạng với tam giác EDF với tỉ số đồng dạng là 1
- Tam giác MPN đồng dạng với tam giác ABC với tỉ số đồng dạng là \(\frac{1}{2}\)
- Tam giác MPN đồng dạng với tam giác EDF với tỉ số đồng dạng là \(\frac{1}{2}\)
(Trả lời bởi Hà Quang Minh)
Vận dụng 2 (SGK Kết nối tri thức với cuộc sống - Trang 96)
Để đón được một người khách, một xe taxi xuất phát từ vị trí điểm A, chạy dọc một con phố dài 3km đến điểm B thì rẽ vuông góc sang trái, chạy được 3km đến điểm C thì tài xế cho xe rẽ vuông góc sang phải, chạy 1km nữa thì gặp người khách tại điểm D (H.9.38). Hỏi lúc đầu, khoảng cách từ chỗ người lái xe đến người khác là bao nhiêu kilômét.
Đọc tiếp
Để đón được một người khách, một xe taxi xuất phát từ vị trí điểm A, chạy dọc một con phố dài 3km đến điểm B thì rẽ vuông góc sang trái, chạy được 3km đến điểm C thì tài xế cho xe rẽ vuông góc sang phải, chạy 1km nữa thì gặp người khách tại điểm D (H.9.38). Hỏi lúc đầu, khoảng cách từ chỗ người lái xe đến người khác là bao nhiêu kilômét.
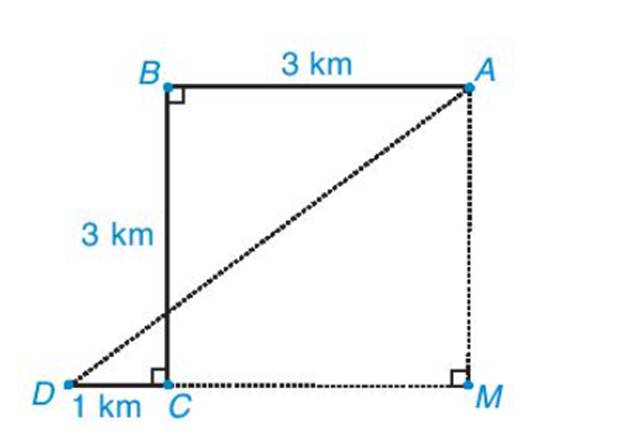
Thảo luận (1)Hướng dẫn giảiTa có: BC=AM=3km
AB=CM=3km
=> MD=CM+CD=3+1=4(km)$
Xét tam giác AMD vuông tại M
=> \(A{{\rm{D}}^2} = A{M^2} + M{{\rm{D}}^2}\)
=> \(A{{\rm{D}}^2} = {3^2} + {4^2}\)
=> AD=5
Vậy lúc đầu, khoảng cách từ chỗ người lái xe đến người khách là 5km
(Trả lời bởi Hà Quang Minh)
Câu hỏi (SGK Kết nối tri thức với cuộc sống - Trang 96)
Cho hình 9.42, trong đó các đoạn thẳng AC, AD, AE đoạn nào có độ dài lớn nhất, đoạn nào có độ dài nhỏ nhất?
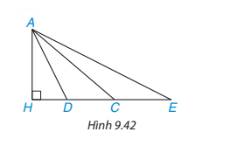
Thảo luận (1)Hướng dẫn giảiÁp dụng định lí Pythagore trong tam giác AHD vuông tại H có: \(A{{\rm{D}}^2} = A{H^2} + H{{\rm{D}}^2}\) (1)
Áp dụng định lí Pythagore trong tam giác AHC vuông tại H có: \(A{C^2} = A{H^2} + H{C^2}\) (2)
Áp dụng định lí Pythagore trong tam giác AHE vuông tại H có: \(A{E^2} = A{H^2} + H{E^2}\) (3)
Vì HE > HC > HD suy ra \(H{E^2} > H{C^2} > H{{\rm{D}}^2}\)(4)
Từ (1), (2), (3), (4) suy ra: \(A{{\rm{E}}^2} > A{C^2} > A{{\rm{D}}^2} \Rightarrow A{\rm{E}} > AC > A{\rm{D}}\)
Vậy đoạn AE là lớn nhất, đoạn AD là nhỏ nhất.
(Trả lời bởi Hà Quang Minh)
Thử thách nhỏ (SGK Kết nối tri thức với cuộc sống - Trang 97)
Tính chiều cao theo đơn vị centimét của một tam giác đều cạnh 2cm (h.9.44) (làm tròn kết quả đến chữ số thập phân thứ hai)
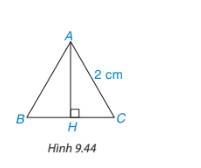
Thảo luận (1)Hướng dẫn giảiVì tam giác ABC là tam giác đều, \(AH \bot BC\) nên H là trung điểm của BC suy ra
\(HB = HC = \frac{{BC}}{2} = \frac{2}{2} = 1\)(cm)
Áp đụng định lí Pythagore trong tam giác AHC ta có:
\(\begin{array}{l}A{C^2} = A{H^2} + H{C^2} \Rightarrow A{H^2} = A{C^2} - H{C^2} = {2^2} - {1^2} = 3\\ \Rightarrow AH = \sqrt 3 \approx 1,73(cm)\end{array}\)
Vậy chiều cao của tam giác đều là 1,73cm.
(Trả lời bởi Hà Quang Minh)
Luyện tập 3 (SGK Kết nối tri thức với cuộc sống - Trang 97)
Trước đây chúng ta thừa nhận định lí về trường hợp bằng nhau đặc biệt của hai tam giác vuông: "Nếu một cạnh góc vuông và cạnh huyền của tam giác vuông này bằng một cạnh góc vuông và cạnh huyền của tam giác vuông kia thì hai tam giác vuông đó bằng nhau”.
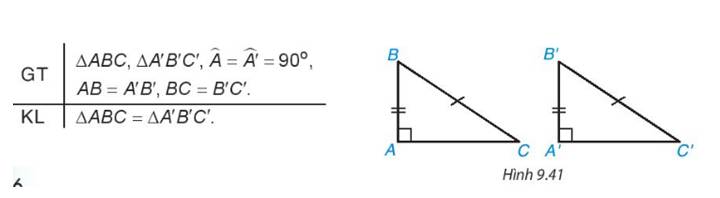
Thảo luận (1)Hướng dẫn giải- Xét tam giác ABC vuông tại A, có
\(\)\(B{C^2} = A{B^2} + A{C^2}\)(1)
- Xét tam giác A'B'C' vuông tại A' có:
\(B'C{'^2} = A'B{'^2} + A'C{'^2}\) (2)
mà AB=A’B’, BC=B’C’ (3)
=> Từ (1), (2), (3): AC= A’C’
=> Hai tam giác bằng nhau
(Trả lời bởi Hà Quang Minh)