a) Một hình vuông có cạnh bằng 3cm. Đường chéo của hình vuông đó bằng : \(6cm,\sqrt{18}cm,5cm\) hay \(4cm\) ?
b) Đường chéo của một hình vuông bằng 2 dm. Cạnh của hình vuông đó bằng : \(1dm,\dfrac{3}{2}dm,\sqrt{2}dm\) hay \(\dfrac{4}{3}dm?\)
Bài 12: Hình vuông
Bài 79 (Sgk tập 1 - trang 108)
Thảo luận (2)
Bài 80 (Sgk tập 1 - trang 108)
Hãy chỉ ró tâm đối xứng của hình vuông, các trục đối xứng của hình vuông ?
Thảo luận (3)Hướng dẫn giảiBài giải:
- Hình vuông là hình chữ nhật có bốn cạnh bằng nhau. Mà hình chữ nhật có tâm đối xứng là giao điểm của hai đường chéo, nên hình vuông có tâm đối xứng là giao điểm của hai đường chéo.
- Hai đường thằng đi qua trung điểm hai cạnh đối của hình chữ nhật là hai trục đối xứng của hình. Mà hình vuông là hình chữ nhật có bốn cạnh bằng nhau nên hai đường trung bình của hình vuông là hai trục đối xứng của nó.
Mặt khác, hai đường chéo của hình thoi là hai trục đối xứng của hình mà hình vuông là hình thoi có bốn góc vuông nên hai đường chéo của hình vuông là hai trục đối xứng của nó.
Vậy hình vuông có bốn trục đối xứng đó là hai đường chéo và hai đường trung bình của hình vuông.
(Trả lời bởi Thien Tu Borum)
Bài 81 (Sgk tập 1 - trang 108)
Cho hình 106. Tứ giác AEDF là hình gì ? Vì sao ?
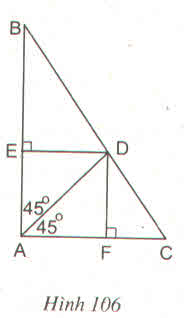
Thảo luận (3)Hướng dẫn giải81. Cho hình 106. Tứ giác AEDF là hình gì ? Vì sao ?
Bài giải:
Tứ giác AEDF là hình vuông.
Giải thích:
Tứ giác AEDF có EA // DF (cùng vuông góc AF)
DE // FA (cùng vuông góc với AE)
nên AEDF là hình bình hành (theo định nghĩa)
Hình bình hành AEDF có đường chéo AD là phân giác của góc A nên là hình thoi.
Hình thoi AEDF có ˆAA^= 900
Nên là hình vuông.
(Trả lời bởi Thien Tu Borum)
Bài 82 (Sgk tập 1 - trang 108)
Cho hình 107, trong đó ABCD là hình vuông. Chứng minh rằng tứ giác EFGH là hình vuông ?
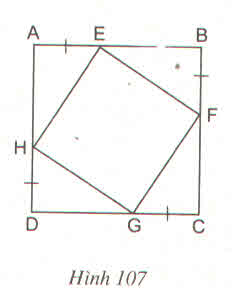
Thảo luận (3)Hướng dẫn giảiBài giải:
Các tam giác vuông AEH, BFC, CGF, DHG có:
AE = BF = CG = DH (gt)
Suy ra AH = BE = CF = DG
Nên ∆AEH = ∆BFE = ∆CGF = ∆DHG (c.g.c)
Do đó HE = EF = FG = GH (1)
và ˆEHAEHA^ = ˆFEBFEB^
Ta có ˆHEFHEF^ = 1800 - (ˆHEAHEA^ + ˆFEBFEB^) = 1800 - (ˆHEAHEA^ + ˆEHAEHA^)
= 1800 - 900 = 900 (2)
Từ (1) và (2) ta được EFGH là hình vuông
(Trả lời bởi Thien Tu Borum)
Luyện tập - Bài 83 (Sgk tập 1 - trang 109)
Các câu đúng hay sai ?
a) Tứ giác có hai đường chéo vuông góc với nhau là hình thoi
b) Tứ giác có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường là hình thoi
c) Hình thoi là tứ giác có tất cả các cạnh bằng nhau
d) Hình chữ nhật có hai đường chéo bằng nhau là hình vuông
e) Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông
Thảo luận (2)Hướng dẫn giải
Luyện tập - Bài 84 (Sgk tập 1 - trang 109)
Cho tam giác ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự ở E và F
a) Tứ giác AEDF là hình gì ? Vì sao ?
b) Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình thoi
c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì ? Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình vuông ?
Đọc tiếp
Cho tam giác ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự ở E và F
a) Tứ giác AEDF là hình gì ? Vì sao ?
b) Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình thoi
c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì ? Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình vuông ?
Thảo luận (1)Hướng dẫn giảia) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt)
(theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ∆ABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật vừa là hình thoi).
(Trả lời bởi Hương Yangg)
Luyện tập - Bài 85 (Sgk tập 1 - trang 109)
Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE
a) Tứ giác ADFE là hình gì ? Vì sao ?
b) Tứ giác EMFN là hình gì ? Vì sao ?
Thảo luận (2)Hướng dẫn giảia) Tứ giác ADFE có AE // DF, AE = DF nên là hình bình hành.
Hình bình hành ADFE có góc A = 900 nên là hình chữ nhật.
Hình chữ nhật ADFE có AE = AD nên là hình vuông.
b) Tứ giác DEBF có EB // DF, EB = DF nên là hình bình hành.
Do đó DE // BF
Tương tự AF // EC
Suy ra EMFN là hình bình hành.
Theo câu a, ADFE là hình vuông nên ME = MF, ME ⊥ MF.
Hình bình hành EMFN có góc M = 900 nên là hình chữ nhật, lại có ME = MF nên là hình vuông.
(Trả lời bởi Hương Yangg)
Luyện tập - Bài 86 (Sgk tập 1 - trang 109)
Đố :
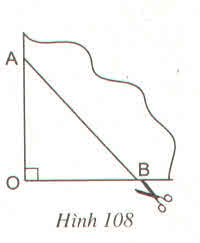
Lấy một tờ giấy gấp làm tư rồi cắt chéo theo nhát cắt (h.108). Sau khi mở tờ giấy ra, ta được một tứ giác. Tứ giác nhận được là hình gì ? Vì sao ? Nếu ta có OA = OB thì tứ giác nhận được là hình gì ?
Thảo luận (1)Hướng dẫn giảiTứ giác nhận được theo nhát cắt AB là hình thoi vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau. Nếu có thêm OA = OB thì hình thoi nhận được có hai đường chéo bằng nhau nên là hình vuông.
(Trả lời bởi Hương Yangg)
Bài 144 (Sách bài tập - trang 98)
Cho tam giác ABC vuông tại A, đường phân giác AD. Gọi M, N theo thứ tự là chân các đường vuông góc kẻ từ D đến AB, AC.
Chứng minh rằng tứ giác AMDN là hình vuông ?
Thảo luận (1)Hướng dẫn giải
Bài 145 (Sách bài tập - trang 98)
Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lấy theo thứ tự các điểm E, K, P, Q sao cho AE = BK = CP = DQ. Tứ giác EKPQ là hình gì ? Vì sao ?
Thảo luận (1)Hướng dẫn giải
AB = BC = CD = DA (gt)
AE = BK = CP = DQ (gt)
Suy ra: EB = KC = PD = QA
- Xét ∆ AEQ và ∆ BKE :
AE = BK (gt)
ˆ
A
=
ˆ
B
=
90
0
A^=B^=900QA = EB (chứng minh trên)
Do đó: ∆ AEQ = ∆ BKE (c.g.c) ⇒ EK = EQ (1)
- Xét ∆ BKE và ∆ CPK :
BK = CP (gt)
ˆ
B
=
ˆ
C
=
90
0
B^=C^=900EB = KC (chứng minh trên)
Do đó: ∆ BKE = ∆ CPK (c.g.c) ⇒ EK = KP (2)
Xét ∆ CPK và ∆ DQP :
CP = DQ (gt)
ˆ
C
=
ˆ
D
=
90
0
C^=D^=900DP = CK (chứng minh trên)
Do đó: ∆ CPK = ∆ DQP (c.g.c) ⇒ KP = PQ (3)
Từ (1), (2) và (3) suy ra: EK = KP = PQ = EQ
Tứ giác EKPQ là hình thoi.
(Trả lời bởi Thanh Ao Tuong)