Cho tam giác vuông cân ABC có AB = AC = a. Tính các tích vô hướng \(\overrightarrow{AB}.\overrightarrow{AC,}\overrightarrow{AC}.\overrightarrow{CB}\) ?
§2. Tích vô hướng của hai vectơ
Bài 1 (SGK trang 45)
Thảo luận (1)
Bài 2 (SGK trang 45)
Cho 3 điểm O, A, B thẳng hàng và biết OA = a; OB = b. Tính tích vô hướng \(\overrightarrow{OA}.\overrightarrow{OB}\) trong hai trường hợp :
a) Điểm O nằm ngoài đoạn AB
b) Điểm O nằm trong đoạn AB
Thảo luận (2)Hướng dẫn giảia) Khi O nằm ngoài đoạn AB thì hai vec tơ
và
cùng hướng và góc
(
,
) = 0
cos(
,
) = 1 nên
.
= a.b
b) Khi O nằm ngoài trongđoạn AB thì hai vectơ
và
ngược hướng và góc
(
,
) = 1800
cos(
,
) = -1 nên
.
= -a.b
(Trả lời bởi Anh Triêt)
Bài 3 (SGK trang 45)
Cho nửa đường tròn tâm O có đường kính AB2R. Gọi M và N là hai điểm thuộc nửa đường tròn sao cho hai dây cung AM và BN cắt nhau tại I
a) Chứng minh overrightarrow{AI}.overrightarrow{AM}overrightarrow{AI}.overrightarrow{AB} và overrightarrow{BI}.overrightarrow{BN}overrightarrow{BI}.overrightarrow{BA}
b) Hãy dùng kết quả câu a) để tính overrightarrow{AI}.overrightarrow{AM}+overrightarrow{BI}.overrightarrow{BN} theo R
Đọc tiếp
Cho nửa đường tròn tâm O có đường kính \(AB=2R\). Gọi M và N là hai điểm thuộc nửa đường tròn sao cho hai dây cung AM và BN cắt nhau tại I
a) Chứng minh \(\overrightarrow{AI}.\overrightarrow{AM}=\overrightarrow{AI}.\overrightarrow{AB}\) và \(\overrightarrow{BI}.\overrightarrow{BN}=\overrightarrow{BI}.\overrightarrow{BA}\)
b) Hãy dùng kết quả câu a) để tính \(\overrightarrow{AI}.\overrightarrow{AM}+\overrightarrow{BI}.\overrightarrow{BN}\) theo R
Thảo luận (1)Hướng dẫn giảia) Nối BM
Ta có AM= AB.cosMAB
=> |
| = |
|.cos(
,
)
Ta có:
.
= |
|.|
| ( vì hai vectơ
,
cùng phương)
=>
.
= |
|.|
|.cosAMB.
nhưng |
|.|
|.cos(
,
) =
.
Vậy
.
=
.
Với
.
=
.
lý luận tương tự.
b)
.
=
.
.
=
.
=>
.
+
.
=
(
+
)
=>
.
+
.
= 4R2
(Trả lời bởi Anh Triêt)
Bài 4 (SGK trang 45)
Trên mặt phẳng Oxy, cho hai điểm \(A\left(1;3\right);B\left(4;2\right)\)
a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB
b) Chứng tỏ OA vuông góc với AB và từ đó tính diện tích tam giác OAB
Thảo luận (2)Hướng dẫn giảiGiải:
a) D nằm trên trục \(Ox\) nên tọa độ của D là \((x; 0).\)
Ta có :
\(DA^2 = (1 - x)^2+ 3^2\)
\(DB^2 = (4 - x)^2+ 2^2\)
\(DA = DB \)
\(\Rightarrow DA^2 = DB^2\)
\(\Leftrightarrow(1-x)^2+9=(4-x)^2+4\)
\(\Leftrightarrow6x = 10\)
\(\Rightarrow x=\dfrac{5}{3}\)
\(\Rightarrow D\)\(\left(\dfrac{5}{3};0\right)\)
b) Ta có:
\(\overrightarrow{OA}= (1; 3)\)
\(\overrightarrow{AP}=\left(3;-1\right)\)
\(1.3 + 3.(-1) = 0 \)
\(\Rightarrow\overrightarrow{OA}=\overrightarrow{OB}=0\)
\(\Rightarrow\overrightarrow{OA}\perp\overrightarrow{AB}\)
SOAB =
(Trả lời bởi Phương Trâm)|
| .|
| => SOAB =5 (dvdt)
Bài 5 (SGK trang 46)
Trên mặt phẳng Oxy hãy tính góc giữa hai vectơ overrightarrow{a} và overrightarrow{b} trong các trường hợp sau :
a) overrightarrow{a}left(2;3right);overrightarrow{b}left(6;4right)
b) overrightarrow{a}left(3;2right);overrightarrow{b}left(5;-1right)
c) overrightarrow{a}left(-2;-2sqrt{3}right);overrightarrow{b}left(3;sqrt{3}right)
Đọc tiếp
Trên mặt phẳng Oxy hãy tính góc giữa hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) trong các trường hợp sau :
a) \(\overrightarrow{a}=\left(2;3\right);\overrightarrow{b}=\left(6;4\right)\)
b) \(\overrightarrow{a}=\left(3;2\right);\overrightarrow{b}=\left(5;-1\right)\)
c) \(\overrightarrow{a}=\left(-2;-2\sqrt{3}\right);\overrightarrow{b}=\left(3;\sqrt{3}\right)\)
Thảo luận (1)Hướng dẫn giảia) cos(
;
) =
= 0
=> (
;
) = 900
b) cos(
;
) =
=
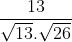
=> (
;
) = 450
c) cos(
;
) =
=
=> (
;
) = 1500
Đăng những câu khác đi em mỏi tay rồi
(Trả lời bởi Anh Triêt)
Bài 6 (SGK trang 46)
Trên mặt phẳng tọa độ Oxy cho 4 điểm \(A\left(7;-3\right);B\left(8;4\right);C\left(1;5\right);D\left(0;-2\right)\). Chứng minh rằng tứ giác ABCD là hình vuông ?
Thảo luận (1)Hướng dẫn giảiTa có:
= (1; 7);
= (1; 7)
=
=> ABCD là hình bình hành (1)
ta lại có : AB2 = 50 => AB = 5 √2
AD2 = 50 => AD = 5 √2
AB = AD, kết hợp với (1) => ABCD là hình thoi (2)
Mặt khác
= (1; 7);
= (-7; 1)
1.7 + (-7).1 = 0 =>
⊥
(3)
(Trả lời bởi Anh Triêt)
Kết hợp (2) và (3) suy ra ABCD là hình vuông
Bài 7 (SGK trang 46)
Trên mặt phẳng Oxy cho điểm \(A\left(-2;1\right)\). Gọi B là điểm đối xứng với điểm A qua gốc tọa độ O. Tìm tọa độ của điểm C có tung độ bằng 2 sao cho tam giác ABC vuông ở C ?
Thảo luận (1)Hướng dẫn giảiĐiểm B đối xứng với A qua gốc tọa độ nên tọa độ của B là (2; -1)
Tọa độ của C là (x; 2). Ta có:
= (-2 - x; -1)
= (-2 - x; -3)
Tam giác ABC vuông tại C =>
⊥
=>
.
= 0
=> (-2 - x)(2 - x) + (-1)(-3) = 0
=> -4 + x2+ 3 = 0
=> x2 = 1 => x= 1 hoặc x= -1
Ta được hai điểm C1(1; 2); C2(-1; 2)
(Trả lời bởi Anh Triêt)
Bài 2.13 (SBT trang 91)
Cho hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) đều khác vectơ \(\overrightarrow{0}\). Tích vô hướng \(\overrightarrow{a}.\overrightarrow{b}\) khi nào dương, khi nào âm và khi nào bằng 0 ?
Thảo luận (1)Hướng dẫn giảiCó \(\overrightarrow{a}.\overrightarrow{b}=\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.cos\left(\overrightarrow{a},\overrightarrow{b}\right)\).
(Trả lời bởi Bùi Thị Vân)
Vì vậy:
\(\overrightarrow{a}.\overrightarrow{b}< 0\) khi \(cos\left(\overrightarrow{a},\overrightarrow{b}\right)< 0\) hay \(90^o< \left(\overrightarrow{a},\overrightarrow{b}\right)\le180^o\).
\(\overrightarrow{a}.\overrightarrow{b}>0\) khi \(cos\left(\overrightarrow{a},\overrightarrow{b}\right)>0\) hay \(0^o\le\left(\overrightarrow{a},\overrightarrow{b}\right)< 90^o\).
\(\overrightarrow{a}.\overrightarrow{b}=0\) khi \(cos\left(\overrightarrow{a},\overrightarrow{b}\right)=0\) hay \(\left(\overrightarrow{a},\overrightarrow{b}\right)=90^o\).
Bài 2.14 (SBT trang 91)
Áp dụng tính chất giao hoán và tính chất phân phối của tích vô hướng hãy chứng minh các kết quả sau đây :
left(overrightarrow{a}+overrightarrow{b}right)^2left|overrightarrow{a}right|^2+left|overrightarrow{b}right|^2+2overrightarrow{a}.overrightarrow{b}
left(overrightarrow{a}-overrightarrow{b}right)^2left|overrightarrow{a}right|^2+left|overrightarrow{b}right|^2-2overrightarrow{a}.overrightarrow{b}
left(overrightarrow{a}+overrightarrow{b}right)left(overrightarrow{a}-overrightarrow{b}right)left|...
Đọc tiếp
Áp dụng tính chất giao hoán và tính chất phân phối của tích vô hướng hãy chứng minh các kết quả sau đây :
\(\left(\overrightarrow{a}+\overrightarrow{b}\right)^2=\left|\overrightarrow{a}\right|^2+\left|\overrightarrow{b}\right|^2+2\overrightarrow{a}.\overrightarrow{b}\)
\(\left(\overrightarrow{a}-\overrightarrow{b}\right)^2=\left|\overrightarrow{a}\right|^2+\left|\overrightarrow{b}\right|^2-2\overrightarrow{a}.\overrightarrow{b}\)
\(\left(\overrightarrow{a}+\overrightarrow{b}\right)\left(\overrightarrow{a}-\overrightarrow{b}\right)=\left|\overrightarrow{a}\right|^2-\left|\overrightarrow{b}\right|^2\)
Thảo luận (1)Hướng dẫn giải\(\left(\overrightarrow{a}+\overrightarrow{b}\right)^2=\left(\overrightarrow{a}+\overrightarrow{b}\right)\left(\overrightarrow{a}+\overrightarrow{b}\right)\)\(=\left|\overrightarrow{a}\right|^2+\left|\overrightarrow{b}\right|^2+2\overrightarrow{a}\overrightarrow{b}\).
(Trả lời bởi Bùi Thị Vân)
\(\left(\overrightarrow{a}-\overrightarrow{b}\right)^2=\left(\overrightarrow{a}-\overrightarrow{b}\right)\left(\overrightarrow{a}-\overrightarrow{b}\right)\)\(=\left|\overrightarrow{a}\right|^2+\left|\overrightarrow{b}\right|^2-2\overrightarrow{a}\overrightarrow{b}\).
\(\left(\overrightarrow{a}-\overrightarrow{b}\right)\left(\overrightarrow{a}+\overrightarrow{b}\right)=\left|\overrightarrow{a}\right|^2+\overrightarrow{a}\overrightarrow{b}-\overrightarrow{a}\overrightarrow{b}+\left|\overrightarrow{b}\right|^2\)\(=\left|\overrightarrow{a}\right|^2-\left|\overrightarrow{b}\right|^2\).
Bài 2.15 (SBT trang 91)
Tam giác ABC vuông cân tại A và có AB = AB = a. Tính
a) \(\overrightarrow{AB}.\overrightarrow{AC}\)
b) \(\overrightarrow{BA}.\overrightarrow{BC}\)
c) \(\overrightarrow{AB}.\overrightarrow{BC}\)
Thảo luận (1)Hướng dẫn giải(Trả lời bởi Bùi Thị Vân)
a) \(\overrightarrow{AB}.\overrightarrow{AC}=0\) do \(AB\perp AC\).
b)
\(BC=\sqrt{AB^2+AC^2}=\sqrt{a^2+a^2}=\sqrt{2}a\).
\(\overrightarrow{BA}.\overrightarrow{BC}=BA.BC.cos\left(\overrightarrow{BA},\overrightarrow{BC}\right)=a.\sqrt{2}a.cos45^o=a^2\).
c) \(\overrightarrow{AB}.\overrightarrow{BC}=-\overrightarrow{BA}.\overrightarrow{BC}=-a^2\).