Cho nửa đường tròn tâm O có đường kính \(AB=2R\). Gọi M và N là hai điểm thuộc nửa đường tròn sao cho hai dây cung AM và BN cắt nhau tại I
a) Chứng minh \(\overrightarrow{AI}.\overrightarrow{AM}=\overrightarrow{AI}.\overrightarrow{AB}\) và \(\overrightarrow{BI}.\overrightarrow{BN}=\overrightarrow{BI}.\overrightarrow{BA}\)
b) Hãy dùng kết quả câu a) để tính \(\overrightarrow{AI}.\overrightarrow{AM}+\overrightarrow{BI}.\overrightarrow{BN}\) theo R
a) Nối BM
Ta có AM= AB.cosMAB
=> |
| = |
|.cos(
, )
Ta có: . = ||.|| ( vì hai vectơ , cùng phương)
=> . = ||.||.cosAMB.
nhưng ||.||.cos(, ) = .
Vậy . = .
Với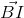 
.
= .
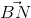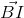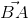lý luận tương tự.
b) . = .
. = .
=> . + . = ( + 
)
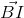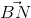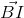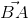
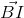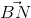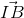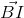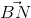=> . + . = 4R2
