§2. Tích vô hướng của hai vectơ
Nội dung lý thuyết
1. Định nghĩa
Cho hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) đều khác \(\overrightarrow{0}\). Tích vô hướng của \(\overrightarrow{a}\) và \(\overrightarrow{b}\) là một số, kí hiệu là \(\overrightarrow{a}.\overrightarrow{b}\), được xác định bởi công thức:
\(\overrightarrow{a}.\overrightarrow{b}=\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.\cos\left(\overrightarrow{a},\overrightarrow{b}\right)\)
Trường hợp ít nhất một trong hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) bằng vectơ \(\overrightarrow{0}\) ta quy ước \(\overrightarrow{a}.\overrightarrow{b}=0\)
Chú ý: +) Với \(\overrightarrow{a}\) và \(\overrightarrow{b}\) khác vectơ \(\overrightarrow{0}\) ta có \(\overrightarrow{a}.\overrightarrow{b}=0\Leftrightarrow\overrightarrow{a}\perp\overrightarrow{b}\)
+) Khi \(\overrightarrow{a}=\overrightarrow{b}\) tích vô hướng \(\overrightarrow{a}.\overrightarrow{a}\) được kí hiệu là \(\overrightarrow{a}^2\) và số này được gọi là bình phương vô hướng của vectơ \(\overrightarrow{a}\).
Ta có: \(\overrightarrow{a}^2=\left|\overrightarrow{a}\right|.\left|\overrightarrow{a}\right|\cos0^0=\left|\overrightarrow{a}\right|^2\)
Ví dụ: Cho tam giác đều \(ABC\) có cạnh bằng \(a\) và có chiều cao \(AH\).
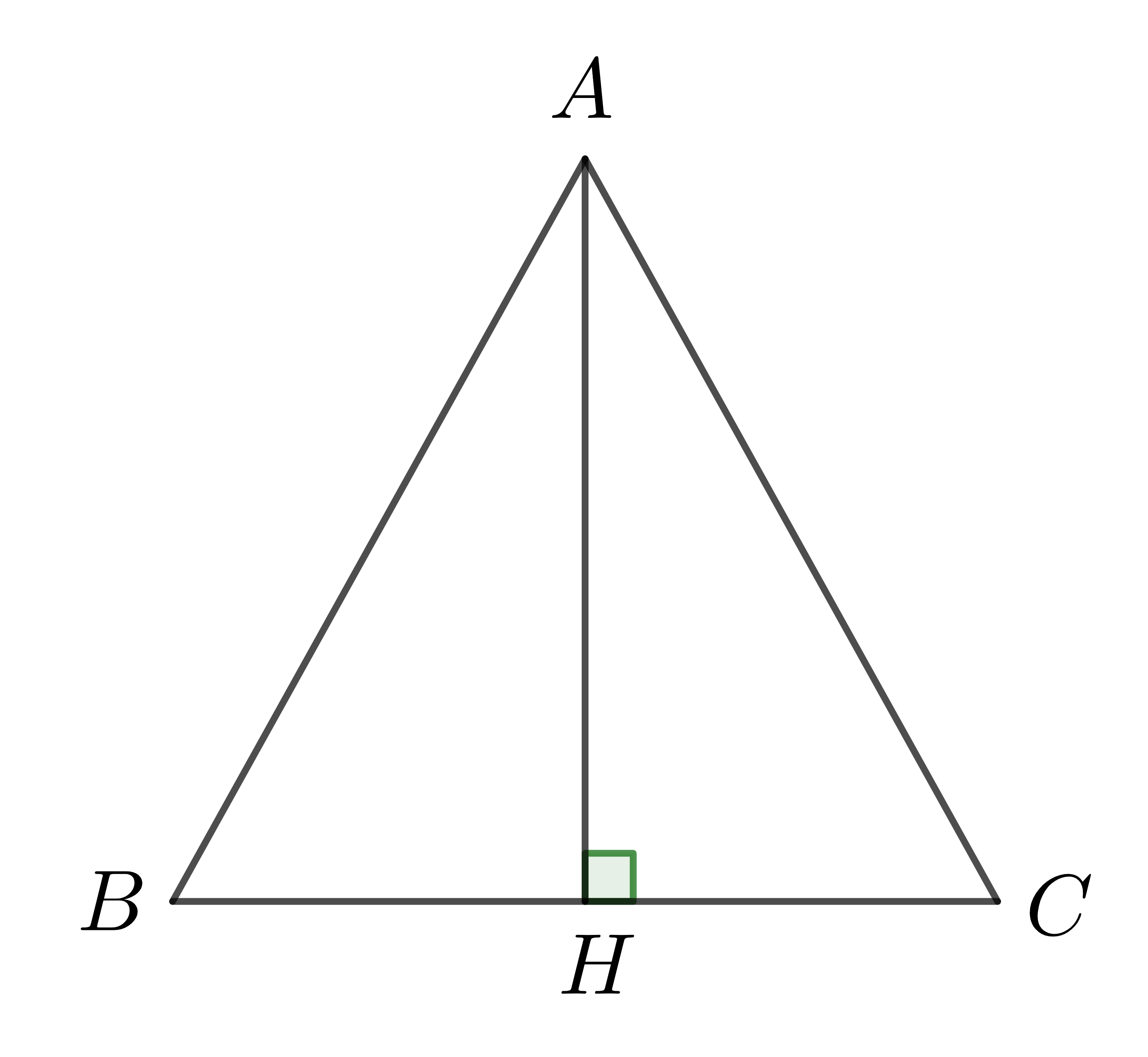
Khi đó ta có: \(\overrightarrow{AB}.\overrightarrow{AC}=a.a.\cos60^0=\dfrac{1}{2}a^2\)
\(\overrightarrow{AC}.\overrightarrow{CB}=a.a.\cos120^0=-\dfrac{1}{2}a^2\)
\(\overrightarrow{AH}.\overrightarrow{BC}=\dfrac{a\sqrt{3}}{2}.a.\cos90^0=0\)
@1956873@
2. Các tính chất của tích vô hướng
Với ba vectơ \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\) bất kì và mọi số \(k\) ta có:
\(\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{a}\) (tính chất giao hoán) ;
\(\overrightarrow{a}.\left(\overrightarrow{b}+\overrightarrow{c}\right)=\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{a}.\overrightarrow{c}\) (tính chất phân phối) ;
\(\left(k\overrightarrow{a}\right).\overrightarrow{b}=k\left(\overrightarrow{a}.\overrightarrow{b}\right)=\overrightarrow{a}.\left(k\overrightarrow{b}\right)\) ;
\(\overrightarrow{a}^2\ge0,\overrightarrow{a}^2=0\Leftrightarrow\overrightarrow{a}=\overrightarrow{0}\).
Nhận xét: Từ các tính chất của tích vô hướng của hai vectơ ta suy ra:
\(\left(\overrightarrow{a}+\overrightarrow{b}\right)^2=\overrightarrow{a}^2+2\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{b}^2\) ;
\(\left(\overrightarrow{a}-\overrightarrow{b}\right)^2=\overrightarrow{a}^2-2\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{b}^2\) ;
\(\left(\overrightarrow{a}+\overrightarrow{b}\right)\left(\overrightarrow{a}-\overrightarrow{b}\right)=\overrightarrow{a}^2-\overrightarrow{b}^2\).
Ứng dụng: Một xe goòng chuyển động từ \(A\) đến \(B\) dưới tác dụng của lực \(\overrightarrow{F}\). Lực \(\overrightarrow{F}\) tạo với hướng chuyển động một góc \(\alpha\), tức là \(\left(\overrightarrow{F},\overrightarrow{AB}\right)=\alpha\).

Lực \(\overrightarrow{F}\) được phân tích thành hai thành phần \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) trong đó \(\overrightarrow{F_1}\) vuông góc với \(\overrightarrow{AB}\), còn \(\overrightarrow{F_2}\) là hình chiếu của \(\overrightarrow{F}\) lên đường thẳng \(AB\). Ta có \(\overrightarrow{F}=\overrightarrow{F_1}+\overrightarrow{F_2}\). Công của lực \(\overrightarrow{F}\) được tính bằng công thức \(\overrightarrow{F}.\overrightarrow{AB}=\left(\overrightarrow{F_1}+\overrightarrow{F_2}\right).\overrightarrow{AB}=\overrightarrow{F_1}.\overrightarrow{AB}+\overrightarrow{F_2}.\overrightarrow{AB}=\overrightarrow{F_2}.\overrightarrow{AB}\).
Như vậy lực thành phần \(\overrightarrow{F_1}\) không làm cho xe gòong chuyển động nên không sinh công. Chỉ có thành phần \(\overrightarrow{F_2}\) sinh công làm cho xe chuyển động từ \(A\) đến \(B\).
Công thức \(\overrightarrow{F}.\overrightarrow{AB}\) là công thức tính công của lực \(\overrightarrow{F}\) làm vật di chuyển từ \(A\) đến \(B\) mà ta học trong vật lí.
3. Biểu thức toạ độ của tích vô hướng
Trên mặt phẳng toạ độ \(\left(O;\overrightarrow{i};\overrightarrow{j}\right)\) cho hai vectơ \(\overrightarrow{a}=\left(a_1;a_2\right)\) và \(\overrightarrow{b}=\left(b_1;b_2\right)\). Khi đó tích vô hướng \(\overrightarrow{a}.\overrightarrow{b}\) là:
\(\overrightarrow{a}.\overrightarrow{b}=a_1b_1+a_2b_2\)
Thật vậy, \(\overrightarrow{a}.\overrightarrow{b}=\left(a_1\overrightarrow{i}+a_2\overrightarrow{j}\right).\left(b_1\overrightarrow{i}+b_2\overrightarrow{j}\right)\)
\(=a_1b_1\overrightarrow{i}^2+a_2b_2\overrightarrow{j}^2+a_1b_2\overrightarrow{i}.\overrightarrow{j}+a_2b_1\overrightarrow{j}.\overrightarrow{i}\)
Vì \(\overrightarrow{i}^2=\overrightarrow{j}^2=1\) và \(\overrightarrow{i}.\overrightarrow{j}=\overrightarrow{j}.\overrightarrow{i}=0\) nên suy ra \(\overrightarrow{a}.\overrightarrow{b}=a_1b_1+a_2b_2\).
Ví dụ 1: Trên mặt phẳng toạ độ \(Oxy\) cho hai vectơ \(\overrightarrow{a}=\left(2;-3\right)\) và \(\overrightarrow{b}=\left(\dfrac{1}{2};1\right)\). Tính tích vô hướng \(\overrightarrow{a}.\overrightarrow{b}\).
Giải:
Áp dụng công thức tính tích vô hướng trên ta có:
\(\overrightarrow{a}.\overrightarrow{b}=2.\dfrac{1}{2}+\left(-3\right).1=1-3=-2\)
Nhận xét: Hai vectơ \(\overrightarrow{a}=\left(a_1;a_2\right)\) và \(\overrightarrow{b}=\left(b_1;b_2\right)\) đều khác vectơ \(\overrightarrow{0}\) vuông góc với nhau khi và chỉ khi \(a_1b_1+a_2b_2=0\).
Ví dụ 2: Trên mặt phẳng toạ độ \(Oxy\) cho các điểm \(A\left(2;4\right)\), \(B\left(1;2\right)\) và \(C\left(6;2\right)\). Chứng minh rằng \(\overrightarrow{AB}\perp\overrightarrow{AC}\).
Giải:
Ta có: \(A\left(2;4\right)\), \(B\left(1;2\right)\) \(\Rightarrow\) \(\overrightarrow{AB}=\left(1-2;2-4\right)=\left(-1;-2\right)\)
\(A\left(2;4\right)\), \(C\left(6;2\right)\) \(\Rightarrow\) \(\overrightarrow{AC}=\left(6-2;2-4\right)=\left(4;-2\right)\)
Nhận thấy \(\left(-1\right).4+\left(-2\right).\left(-2\right)=-4+4=0\)
Suy ra \(\overrightarrow{AB}\perp\overrightarrow{AC}\).
@1958447@
4. Ứng dụng
a) Độ dài của vectơ
Độ dài của vectơ \(\overrightarrow{a}=\left(a_1;a_2\right)\) được tính theo công thức:
\(\left|\overrightarrow{a}\right|=\sqrt{a_1^2+a_2^2}\)
Thật vậy: ta có \(\left|\overrightarrow{a}\right|^2=\overrightarrow{a}^2=\overrightarrow{a}.\overrightarrow{a}=a_1a_1+a_2a_2=a_1^2+a_2^2\)
Do đó \(\left|\overrightarrow{a}\right|=\sqrt{a_1^2+a_2^2}\)
Ví dụ 1: Tính độ dài của các vectơ \(\overrightarrow{u}=\left(1;7\right)\) và \(\overrightarrow{v}=\left(5;-5\right)\).
Giải:
Áp dụng công thức tính độ dài vectơ trên ta có:
\(\left|\overrightarrow{u}\right|=\sqrt{1^2+7^2}=\sqrt{50}=5\sqrt{2}\)
\(\left|\overrightarrow{v}\right|=\sqrt{5^2+\left(-5\right)^2}=\sqrt{50}=5\sqrt{2}\)
@1958536@
b) Góc giữa hai vectơ
Từ định nghĩa tích vô hướng của hai vectơ ta suy ra nếu \(\overrightarrow{a}=\left(a_1;a_2\right)\) và \(\overrightarrow{b}=\left(b_1;b_2\right)\) đều khác \(\overrightarrow{0}\) thì ta có:
\(\cos\left(\overrightarrow{a},\overrightarrow{b}\right)=\dfrac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}=\dfrac{a_1b_1+a_2b_2}{\sqrt{a_1^2+a_2^2}.\sqrt{b\text{}\text{}_1^2+b_2^2}}\)
Ví dụ 2: Cho \(\overrightarrow{OM}=\left(-2;-1\right)\), \(\overrightarrow{ON}=\left(3;-1\right)\). Tính \(\left(\overrightarrow{OM},\overrightarrow{ON}\right)\).
Giải:
Ta có: \(\cos\widehat{MON}=\cos\left(\overrightarrow{OM},\overrightarrow{ON}\right)=\dfrac{\overrightarrow{OM}.\overrightarrow{ON}}{\left|\overrightarrow{OM}\right|.\left|\overrightarrow{ON}\right|}\)
\(=\dfrac{\left(-2\right).3+\left(-1\right).\left(-1\right)}{\sqrt{\left(-2\right)^2+\left(-1\right)^2}.\sqrt{3^2+\left(-1\right)^2}}=\dfrac{-6+1}{\sqrt{5}.\sqrt{10}}=-\dfrac{\sqrt{2}}{2}\)
Như vậy \(\cos\left(\overrightarrow{OM},\overrightarrow{ON}\right)=-\dfrac{\sqrt{2}}{2}\) \(\Rightarrow\) \(\left(\overrightarrow{OM},\overrightarrow{ON}\right)=135^0\)
Vậy \(\left(\overrightarrow{OM},\overrightarrow{ON}\right)=135^0\).
@1957144@
c) Khoảng cách giữa hai điểm
Khoảng cách giữa hai điểm \(A\left(x_A;y_A\right)\) và \(B\left(x_B;y_B\right)\) được tính theo công thức:
\(AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}\)
Thật vậy, với \(A\left(x_A;y_A\right)\) và \(B\left(x_B;y_B\right)\) ta có \(\overrightarrow{AB}=\left(x_B-x_A;y_B-y_A\right)\)
Nên \(AB=\left|\overrightarrow{AB}\right|=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}\).
Ví dụ 3: Cho hai điểm \(M\left(-2;2\right)\) và \(N\left(1;1\right)\). Tính độ dài đoạn thẳng \(MN\).
Giải:
Áp dụng công thức tính độ dài đoạn thẳng trên ta có:
\(MN=\sqrt{\left(1-\left(-2\right)\right)^2+\left(1-2\right)^2}=\sqrt{3^2+\left(-1\right)^2}=\sqrt{10}\)
Vậy \(MN=\sqrt{10}\).