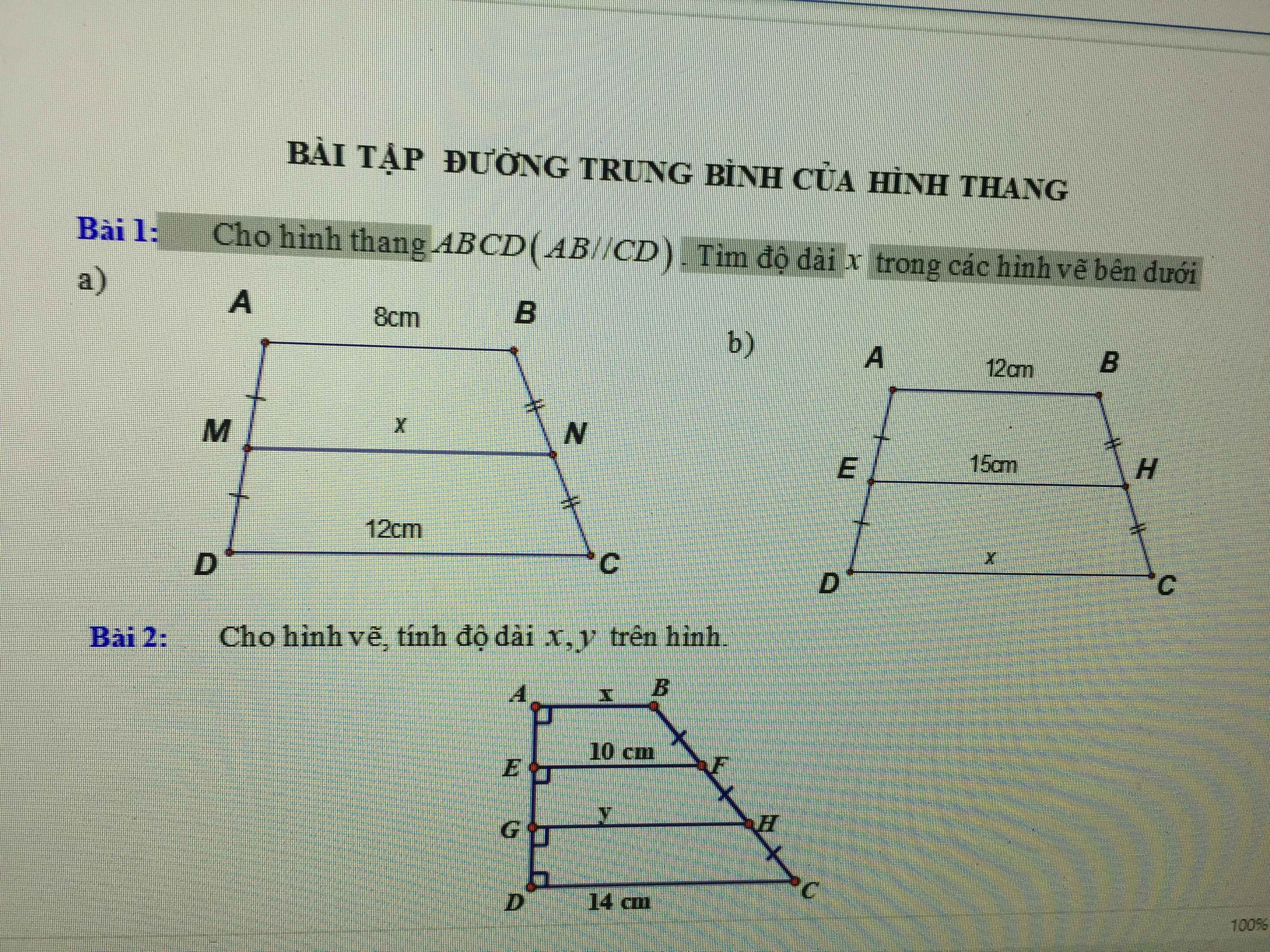
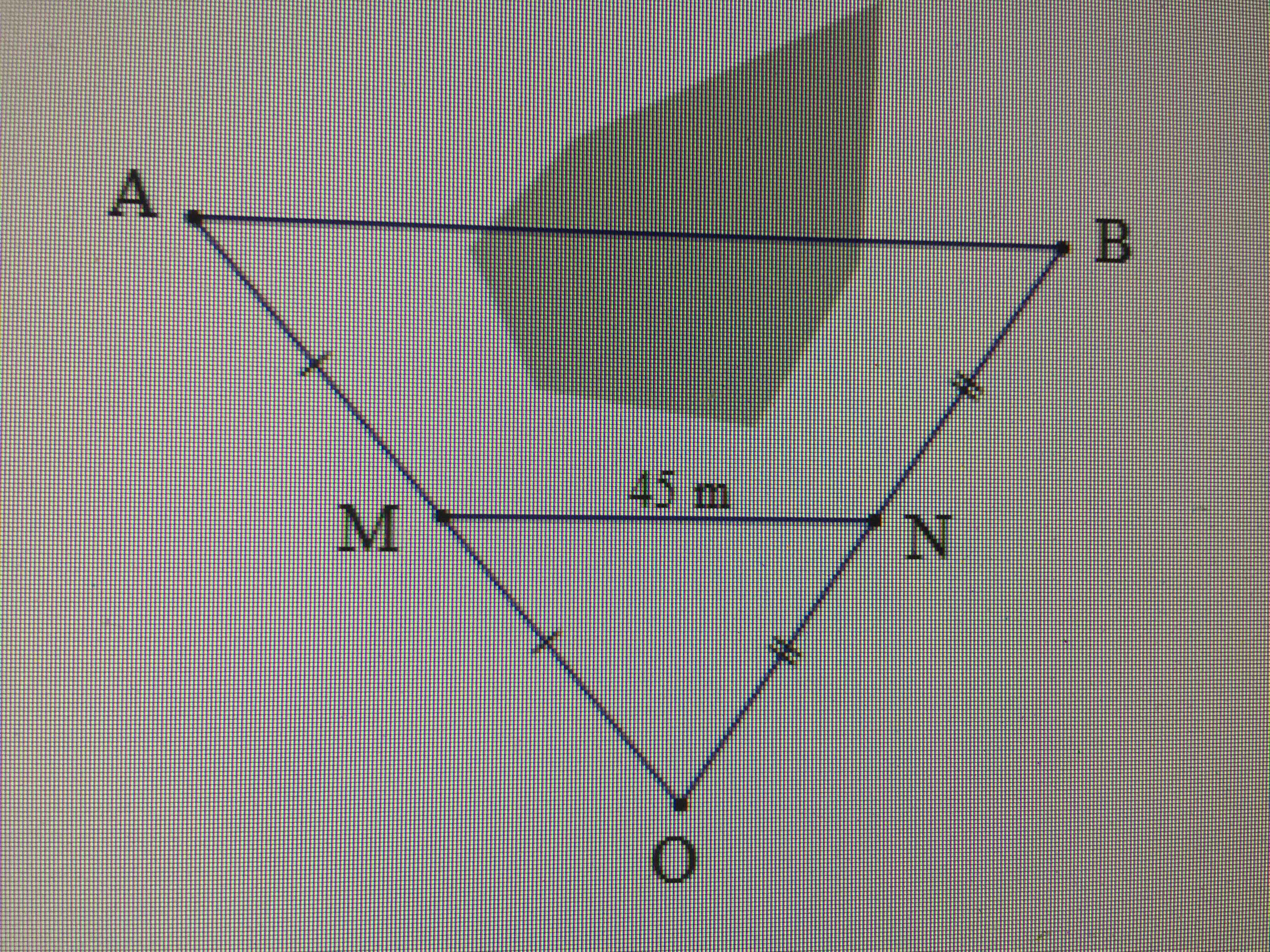
Đề : Cho \(\Delta ABC\) vuông tại A. Gọi M, N lần lượt là trung điểm của AB, BC. Biết \(AB=5cm\), \(AC=12cm\). Tính MN và AN
Hình:

Vẽ hình giúp rồi ai đó làm đi.
Áp dụng định lí pitago cho Δ ABC vuông tại A ta có
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC^2=5^2+12^2\)
\(\Rightarrow BC^2=169\)
\(\Rightarrow BC=13\left(cm\right)\)
ΔABC vuông tại A có
AN là đường trung tuyến ứng với cạnh huỳên BC ( N là trung điểm BC)
\(\Rightarrow AN=\dfrac{1}{2}BC\) ( trong tam giác vuông đường trung tuyến ứng với cạnh huyền thì bằng 1 nủă cạnh huyền )
\(\Rightarrow AN=\dfrac{1}{2}.13\)
\(\Rightarrow AN=6.5\left(cm\right)\)
Δ ABC có
M là trung điểm AB ( gt)
N là trung điểm BC (gt)
\(\Rightarrow MN\) là đường trung bình cua tam giác ABC
\(\Rightarrow MN=\dfrac{1}{2}AC\)
\(\Rightarrow MN=6\left(cm\right)\)
Vậy AN = 6.5 cm và MN = 6cm
AD điinh lý pitago vào tam giác vuông ABC , có :
AB2 + AC2 = BC2
52 + 122 = BC2
25 + 144 = BC2
169 = BC2
=> BC = \(\sqrt{169}\)= 13
Trong tam giác vuông ABC , có :
MA = MB ( GT)
NA = NC ( GT)
=> NM là đường TB của tam giác vuông ABC
=> MN = \(\dfrac{1}{2}\) . BC = \(\dfrac{1}{2}\). 13 = 6,5
Vậy MN = 6,5 cm
Ta có : N là trung điểm của AC
=> AN = \(\dfrac{1}{2}\). AC = \(\dfrac{1}{2}\).12 = 6
Vậy ÂN = 6cm