Lời giải:
$y=(3x+6)^5(-x+1)$
$y'=-9(3x+6)^4(2x-1)$
$y'=0\Leftrightarrow x=-2$ hoặc $x=\frac{1}{2}$
Lập BBT ta thấy hàm đồng biến trên $(-\infty; \frac{1}{2})$ và nghịch biến trên $(\frac{1}{2};+\infty)$
Lời giải:
$y=(3x+6)^5(-x+1)$
$y'=-9(3x+6)^4(2x-1)$
$y'=0\Leftrightarrow x=-2$ hoặc $x=\frac{1}{2}$
Lập BBT ta thấy hàm đồng biến trên $(-\infty; \frac{1}{2})$ và nghịch biến trên $(\frac{1}{2};+\infty)$
Xét tính đơn điệu của hàm số:
y= x4- 2x2
Xét tính đơn điệu của hàm số: f(x) = 2x - sin2x
Xét tính đơn điệu của hàm số: f(x) = x + |3x2 + 9x -12|
Xét tính đơn điệu của hàm số: f(x) = x +\(\sqrt{x^2-4}\)
xét tính đơn điệu của hàm số y=\(\dfrac{-x^2+2x-1}{x+2}\)
Giúp em 2 câu này vs ạ
Đề: xét tính đơn điệu của hàm số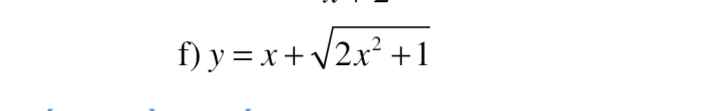
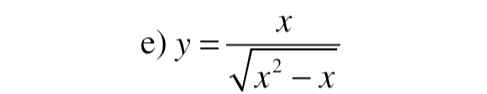
Xét tính đơn điệu của hàm số (có vẽ bảng biến thiên)
\(y = \sqrt{2x - x^3}\)
xét tính đơn điệu của hàm số y=sin(1/x), x>0.
Xét tính đơn điệu của hàm số:
a, f(x) = x + 2cosx trên (0;2π)
b, f(x) = |x2 - 3x + 2|