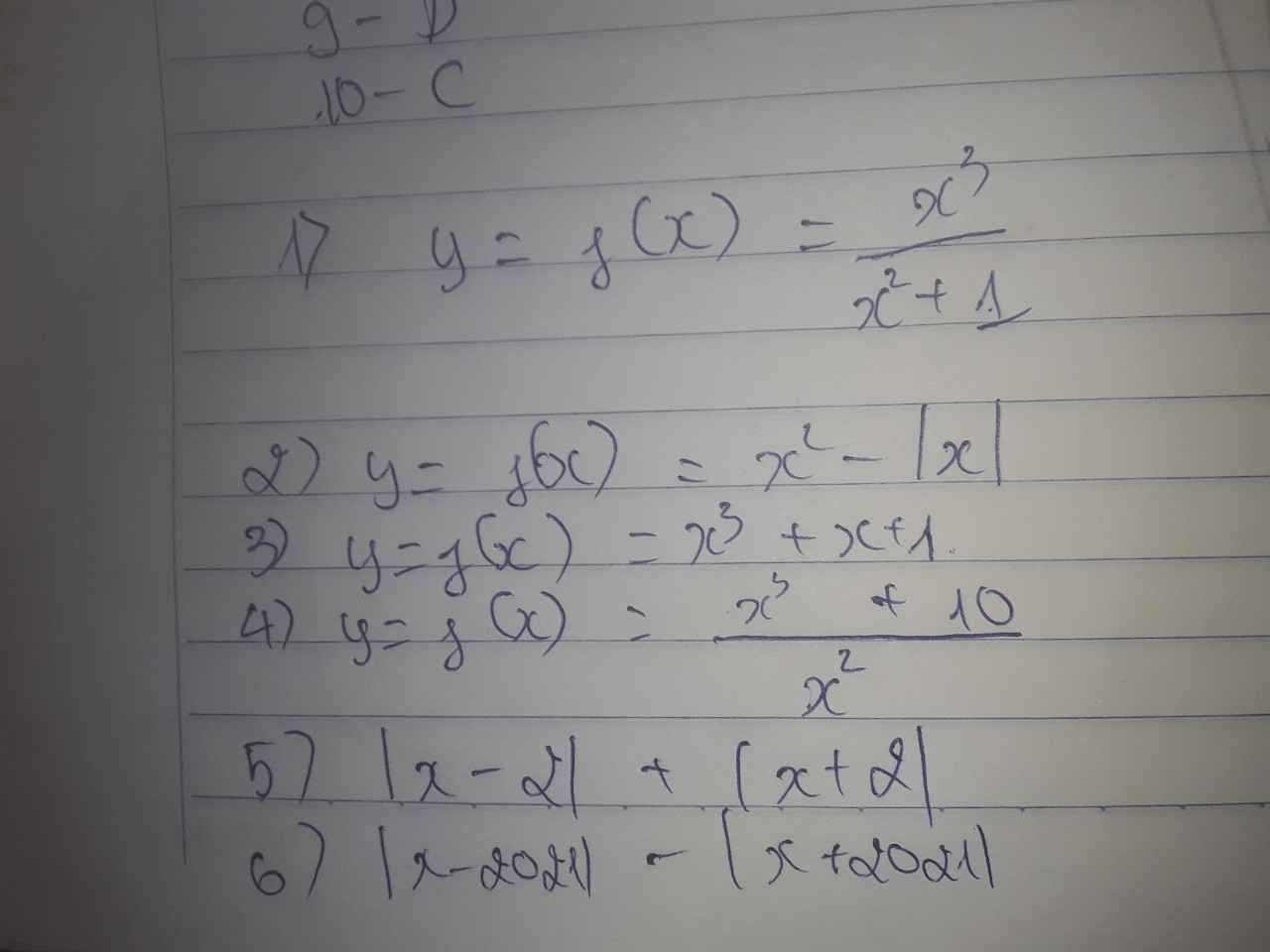Lời giải:
TXĐ: $D=\mathbb{R}$
Lấy $x_1\neq x_2\in D$. Xét:
$A=\frac{f(x_1)-f(x_2)}{x_1-x_2}$
\(=\frac{\frac{x_1^3}{x_1^2+1}-\frac{x_2^3}{x_2^2+1}}{x_1-x_2}=\frac{x_1^2x_2^2+x_1^2+x_1x_2+x_2^2}{(x_1^2+1)(x_2^2+1)}>0\) với mọi $x_1,x_2\in\mathbb{R}; x_1\neq x_2$
Do đó hàm số luôn đồng biến trên $\mathbb{R}$