\(9x^2-y^2\\ =\left(3x\right)^2-y^2\\ =\left(3x-y\right)\left(3x+y\right)\)
\(9x^2\) - \(y^2\) = \(\left(3x\right)^2\) - \(y^2\) = ( 3x + y )( 3x - y )
( Hằng đẳng thức Hiệu của hai bình phương )
Viết các biểu thức sau thành đa thức:
a) \(\left( {a - 5} \right)\left( {{a^2} + 5a + 25} \right)\) b) \(\left( {x + 2y} \right)\left( {{x^2} - 2xy + 4{y^2}} \right)\)
Viết các biểu thức sau thành bình phương của một tổng hoặc một hiệu:
a) \({a^2} + 10ab + 25{b^2}\) b) \(1 + 9{a^2} - 6a\)
a) Viết biểu thức tính diện tích của hình vuông có cạnh bằng 2x+3dưới dạng đa thức
b) Viết biểu thức tính thể tích của khối lập phương có cạnh bằng 3x−2dưới dạng đa thức.
Viết các biểu thức sau thành đa thức:
a) \(\left( {a - 1} \right)\left( {a + 1} \right)\left( {{a^2} + 1} \right)\) b) \({\left( {xy + 1} \right)^2} - {\left( {xy - 1} \right)^2}\)
Viết các đa thức sau dưới dạng tích:
a) \(8{y^3} + 1\) b) \({y^3} - 8\)
Viết các biểu thức sau thành đa thức:
a) \(\left( {3x - 5} \right)\left( {3x + 5} \right)\) b) \(\left( {x - 2y} \right)\left( {x + 2y} \right)\) c) \(\left( { - x - \dfrac{1}{2}y} \right)\left( { - x + \dfrac{1}{2}y} \right)\)
a) Từ Hình 3a, người ta cắt ghép tạo thành Hình 3b. Viết hai biểu thức khác nhau, mỗi biểu thức biểu thị diện tích (phần tô màu) của một trong hai hình bên.
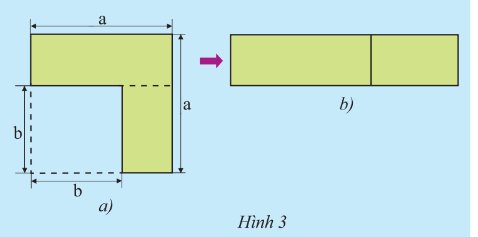
b) Thực hiện phép nhân và rút gọn đa thức, biến đổi biểu thức \(\left( {a + b} \right)\left( {a - b} \right)\) thành một đa thức thu gọn. Từ đó, có kết luận gì về diện tích của hai hình bên?
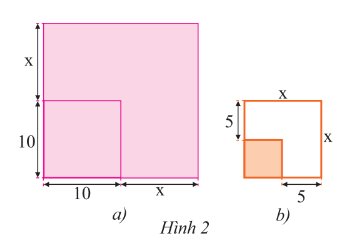
a) Một mảnh vườn hình vuông có cạnh \(10\)m được mở rộng cả hai cạnh thêm \(x\) (m) như Hình 2a. Viết biểu thức (dạng đa thức thu gọn) biểu thị diện tích mảnh vườn sau khi mở rộng.
b) Một mảnh vườn hình vuông sau khi mở rộng mỗi cạnh \(5\)m thì được một mảnh vườn hình vuông có cạnh là \(x\) (m) như Hình 2b. Viết biểu thức (dạng đa thức thu gọn) biểu thị diện tích mảnh vườn trước khi mở rộng.
Viết các biểu thức sau thành bình phương của một tổng hoặc một hiệu:
a) \({x^2} + 2x + 1\) b) \(9 - 24x + 16{x^2}\) c) \(4{x^2} + \dfrac{1}{4} + 2x\)
Viết các biểu thức sau thành đa thức:
a) \({\left( {2x - 3} \right)^3}\) b) \({\left( {a + 3b} \right)^3}\) c) \({\left( {xy - 1} \right)^3}\)
