M cách đầu E và F =>M là trung điểm của EF
Gọi tọa độ điểm M là M(xM;yM)
=>\(x_M=\frac{x_E+x_F}{2}=\frac{0+4}{2}=2;y_M=\frac{y_E+y_F}{2}=\frac{4-9}{2}=-\frac{5}{2}\)
Vậy M(2;-5/2)
Gọi điểm cần tìm trên (d) là M thì M có tọa độ dạng: M=(x; x+2).
Theo giả thiết: MA=MB <=> MA^2=MB^2
Dùng công thức khoảng cách có ptrình:
(x-0)^2 + (x+2 - 4)^2 = (x-4)^2 + (x+2 +9)^2
Giải ptrình này có: x=-133/18.
Vậy M=(-133/18; -97/18)
Hương Trà ơi , tại sao M lại có tọa độ (x,x+2) vậy ?
Vì nó thuộc (d)
Y=x+2
Nên M có toạ đọ như thế
Đường thẳng (d) qua E(0,4) và F(4,-9) có dạng: y = ax + b. thay tọa độ E, F vào có:
{ 4 = a.0 + b
{ - 9 = a.4 + b
=> b = 4; a = -13/4
=> pt của (d) là : 13x + 4y - 16 = 0
M cách đều E, F nên thuộc đường thẳng trung trực (d') của EF. Gọi I là trung điểm EF có tọa độ của I là :
{ xi = (xE + xF)/2 = (0 + 4)/2 = 2
{ yi = (yE + yF)/2 = (4 + (-9))/2 = -5/2
(d') vuông góc (d) nên Pt của (d') có dạng 4x - 13y + c' = 0
(d') qua I(2,-5/2) nên : 4.2 - 13.(-5/2) + c' = 0 => c' = - 61/2
=> pt của (d') là : 8x - 26y - 61 = 0
M vừa thuộc delta, vừa thuộc (d') nên là nghiệm của hệ:
{ x - y +2 = 0
{ 8x - 26y - 61 = 0
Giải ra x = 41/18; y = 77/18
Vậy M(41/18; 77/18) là điểm cần tìm










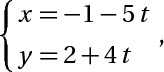 d2:
d2: 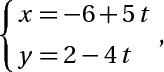
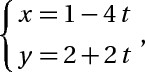 d2 : 2x+4y-10=0
d2 : 2x+4y-10=0 