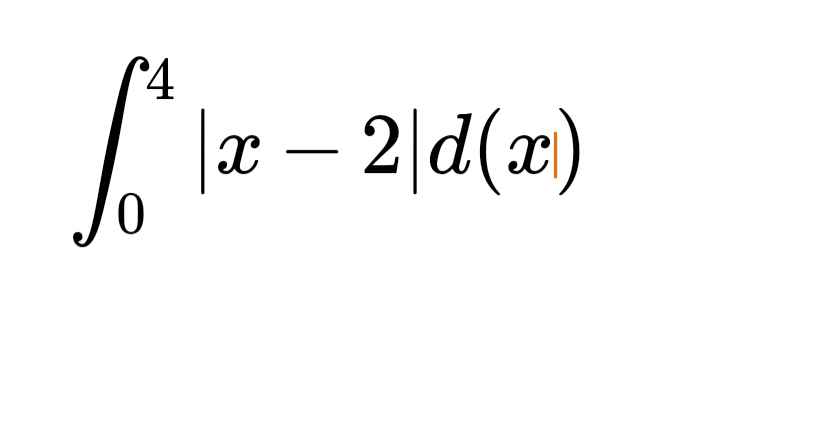Question

Tính tích phân

Answer 1

Giúp mình với các bạn ơi

Answer 2

ANH CHỊ THAM KHẢO:

Answer 3

\(\int\limits^4_0\left|x-2\right|dx=\int\limits^2_0\left|x-2\right|dx+\int\limits^4_2\left|x-2\right|dx\)

\(=\int\limits^2_0\left(2-x\right)dx+\int\limits^4_2\left(x-2\right)dx\)

\(=\left(2x-\dfrac{1}{2}x^2\right)|^2_0+\left(\dfrac{1}{2}x^2-2x\right)|^4_2=...\)