Thay x = 4 vào \(\frac {x+2}{x-1}\) ta được:
\(\frac {4+2}{4-1} = \frac {6}{3} = 2\)
Tại x=4 thì biểu thức trên bằng:
\(\dfrac{x+2}{x-1}=\dfrac{4+2}{4-1}=\dfrac{6}{3}=2\)
Vậy tại x=4 thì giá trị biểu thức bằng 2
Thay x = 4 vào \(\frac {x+2}{x-1}\) ta được:
\(\frac {4+2}{4-1} = \frac {6}{3} = 2\)
Tại x=4 thì biểu thức trên bằng:
\(\dfrac{x+2}{x-1}=\dfrac{4+2}{4-1}=\dfrac{6}{3}=2\)
Vậy tại x=4 thì giá trị biểu thức bằng 2
Cho phân thức: \(\dfrac{{x + 1}}{{{x^2} + x}}\)
a) Viết điều kiện của x để giá trị của phân thức được xác định.
b) Tính giá trị của phân thức tại x = 10 và x = -1.
Cho phân thức: \(\dfrac{{2{{\rm{x}}^2} - x + 1}}{{x - 2}}\). Tìm giá trị của x sao cho mẫu: \(x - 2 \ne 0\).
Cho biểu thức: \(\dfrac{{2{\rm{x}} + 1}}{{x - 2}}\)
a) Biểu thức 2x +1 ở tử có phải là đa thức hay không?
b) Biểu thức x – 2 ở mẫu có phải là đa thức khác đa thức 0 hay không?
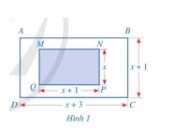
Cho hình chữ nhật ABCD và MNPQ như hình 1 (các số đo trên hình tính theo đơn vị centimét).
a) Viết phân thức biểu thị tỉ số diện tích của hình chữ nhật ABCD và hình chữ nhật MNPQ.
b) Tính giá trị của phân thức đó tại x = 2 và tại x = 5.
Trong các biểu thức sau, biểu thức nào là phân thức?
\(a)\dfrac{{{x^2}y + x{y^2}}}{{x - y}}\) \(b)\dfrac{{{x^2} - 2}}{{\dfrac{1}{x}}}\)
Cho hai phân thức \(\dfrac{1}{{{x^2}y}}\) và \(\dfrac{1}{{x{y^2}}}\)
a) Hãy nhân cả tử và mẫu của phân thức thứ nhất với y và nhân cả tử và mẫu của phân thức thứ hai với x.
b) Nhân xét gì về mẫu của hai phân thức thu được.
Quy đồng mẫu thức hai phân thức \(\dfrac{1}{x^2+x}\) và \(\dfrac{1}{x^2-x}\).
Mỗi cặp phân thức sau có bằng nhau không? Vì sao?
a) \(\dfrac{{x + y}}{{{x^2} - {y^2}}}\) và \(\dfrac{1}{{x - y}}\)
b) \(\dfrac{x}{{{x^2} - 1}}\) và \(\dfrac{1}{{x - 1}}\)
Quy đồng mẫu thức các phân thức trong mỗi trường hợp sau:
a) \(\dfrac{5}{{2{{\rm{x}}^2}{y^3}}}\) và \(\dfrac{3}{{x{y^4}}}\)
b) \(\dfrac{3}{{2{{\rm{x}}^2} - 10{\rm{x}}}}\) và \(\dfrac{2}{{{x^2} - 25}}\)