Question

Tính diện tích hình phẳng giới hạn bởi các đường:

a) y = X², y = x + 2;    b) y = |lnx|, y = 1; c) y = (x – 6)², y = 6x– x²

 

 

Answer 1

a) Phương trình hoành độ giao điểm f(x) =  X² - x - 2 =0 ⇔ x = -1 hoặc x = 2.

Diện tích hình phẳng cần tìm là :

    

    

b) Phương trình hoành độ giao điểm: 

f(x) = 1 - ln|x| = 0  ⇔ lnx = ± 1

⇔ x = e hoặc                                                       

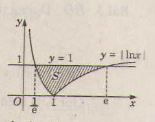
        y = ln|x| = lnx nếu lnx ≥ 0 tức là x ≥ 1.

 hoặc  y = ln|x| = - lnx nếu x < 0, tức là 0 < x < 1.

Dựa vào đồ thị hàm số vẽ ở hình trên ta có diện tích cần tìm là :  

    

     

     

Ta có  ∫lnxdx = xlnx - ∫dx = xlnx  –  x  + C,  thay vào trên ta được  :

 

    

c) Phương trình hoành độ giao điểm là:

f(x) = 6x  –  x² – (x - 6)²  = -2(x² – 9x +18)