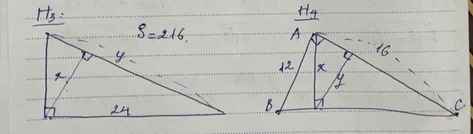
H3: Giả sửa là tam giác ABC vuông tại A có đường cao AH,Cần tính BC và AH biết diện tích tam giác là 216 và \(AC=24\)
Ta có: \(S_{ABC}=\dfrac{1}{2}AB.AC\Rightarrow216=\dfrac{1}{2}.AB.24\Rightarrow AB=18\)
Vì tam giác ABC vuông tại A có đường cao AH
\(\Rightarrow\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{AH^2}\Rightarrow\dfrac{1}{18^2}+\dfrac{1}{24^2}=\dfrac{1}{AH^2}\)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{25}{5184}\Rightarrow AH^2=\dfrac{5184}{25}\Rightarrow AH=\dfrac{72}{5}\Rightarrow x=\dfrac{72}{5}\)
Ta có: \(AH.BC=AB.AC\Rightarrow18.24=\dfrac{72}{5}.BC\Rightarrow BC=30\Rightarrow y=30\)
H4: Giả sửa là tam giác ABC vuông tại A có đường cao AH,kẻ \(HD\bot AC\)
Cần tính \(AH,HD\) biết \(AB=12,AC=16\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=20\)
Ta có: \(AH.BC=AB.AC\Rightarrow12.16=AH.20\Rightarrow AH=\dfrac{48}{5}\Rightarrow x=\dfrac{48}{5}\)
Ta có: \(AC^2=CH.BC\Rightarrow16^2=CH.20\Rightarrow CH=\dfrac{64}{5}\)
Vì \(HD\parallel AB(\bot AC)\) \(\Rightarrow\dfrac{CH}{CB}=\dfrac{HD}{AB}\Rightarrow\dfrac{\dfrac{64}{5}}{20}=\dfrac{HD}{12}\Rightarrow HD=\dfrac{192}{25}\)
\(\Rightarrow y=\dfrac{192}{25}\)