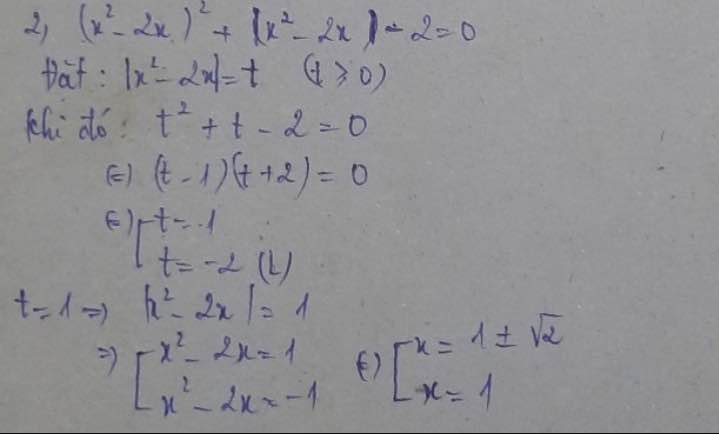Question

Tìm \(x\):

\(\left(x^2+2x\right)^2+\left|x^2+2x\right|-2=0\)

Answer 1

Answer 2

Ta có: \(\left(x^2+2x\right)^2+\left|x^2+2x\right|-2=0\)

\(\Leftrightarrow\left(\left|x^2+2x\right|-1\right)\left(\left|x^2+2x\right|+2\right)=0\)

\(\Leftrightarrow\left|x^2+2x\right|=1\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2+2x+1=0\\x^2+2x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left(x+1\right)^2=0\\\left(x+1\right)^2=2\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x+1=\sqrt{2}\\x+1=-\sqrt{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\sqrt{2}-1\\x=-\sqrt{2}-1\end{matrix}\right.\)