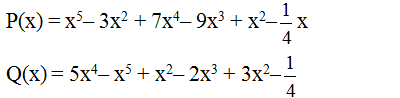Ta có: \(P\left(x\right)=0\)
\(\Rightarrow\left(x-2\right)\left(x^2+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x^2+2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2\\x^2=-2\end{matrix}\right.\)
mà \(x^2\ge0\forall x\)
=> Đa thức P (x) có một nghiệm là 2.
Ta có: P(x)=0 \(\Rightarrow\left(x-2\right).\left(x^2+2\right)=0\)
=> x-2=0 hoặc \(x^2+2=0\)
+,x-2=0 => x=2 (1)
+,\(x^2+2=0\)
Với mọi giá trị của \(x\in R\) ta có: \(x^2\ge0\Rightarrow x^2+2\ge2>0\)
không tìm được giá trị nào của x để biểu thức \(x^2+2=0\) (2)
Từ (1) và (2) suy ra: x=2
Vậy nghiệm của đa thức P(x) là 2
Chúc bạn học tốt nha!!
Cho \(\left(x-2\right)\left(x^2+2\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x-2=0\\x^2+2=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\x=\sqrt{2}\end{matrix}\right.\)
Xét \(P\left(x\right)=\left(x-2\right)\left(x^2+2\right)=0\)
\(\left(x-2\right)\left(x^2+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-2=0\\x^2+2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=\sqrt{2}\end{matrix}\right.\)
Vậy, ...
\(P\left(x\right)=\left(x-2\right)\left(x^2+2\right)\)
Ta có: \(\left(x-2\right)\left(x^2+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-2=0\\x^2+2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2\\x^2=-2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2\\x=-\sqrt{2}\end{matrix}\right.\)
Vậy \(x=2;x=-\sqrt{2}\) là nghiệm của P(x)
\(P\left(x\right)=\left(x-2\right)\left(x^2+2\right)\)
Ta có:
\(\left(x-2\right)\left(x^2+2\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-2=0\\x^2+2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2\\x\in\varnothing\end{matrix}\right.\)
Vậy x=2 là nghiệm của đa thức trên.