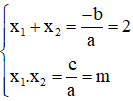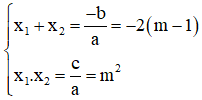a) Phương trình \(x^2-2x+m\) có nghiệm khi ∆' = 1 - m ≥ 0 hay khi m ≤ 1
Khi đó \(x_1+x_2=2,x_1.x_2=m\)
b) Phương trình \(x^2-2\left(m-1\right)x+m^2=0\)có nghiệm khi
\(\text{∆}'=m^2-2m+1-m^2=1-2m\ge0\)' hay khi m \(\le\dfrac{1}{2}\)
Khi đó \(x_1+x_2=-2\left(m-1\right),x_1.x_2=m^2\)
a) Phương trình x^2 – 2x + m = 0
Có a = 1; b = -2; c = m
⇒ Δ’ = (-1)^2 – 1.m = 1 – m
Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ 1 – m ≥ 0 ⇔ m ≤ 1.
Khi đó, theo định lý Vi-et:
Vậy với m ≤ 1, phương trình có hai nghiệm có tổng bằng 2; tích bằng m.
b) Phương trình x^2 + 2(m – 1)x + m^2 = 0
Có a = 1; b = 2(m – 1); c = m^2
⇒ Δ’ = b'2 – ac = (m – 1)^2 – m^2 = 2m – 1.
Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ 2m – 1 ≥ 0 ⇔ m ≥ 1/2.
Khi đó, theo định lý Vi-et:
Vậy với m ≥ ½, phương trình có hai nghiệm có tổng bằng -2(m – 1), tích bằng m2.
Lời giải:
a) Phương trình \({x^2}-{\rm{ }}2x{\rm{ }} + {\rm{ }}m{\rm{ }} = {\rm{ }}0\) có nghiệm khi \(\Delta '{\rm{ }} = {\rm{ }}1{\rm{ }} - {\rm{ }}m{\rm{ }} \ge {\rm{ }}0\) hay khi \(m ≤ 1\)
Khi đó \({x_{1}} + {\rm{ }}{x_{2}} = {\rm{ }}2\), \({\rm{ }}{x_{1}}.{\rm{ }}{x_2} = {\rm{ }}m\)
b) Phương trình \({x^2}-{\rm{ }}2\left( {m{\rm{ }}-{\rm{ }}1} \right)x{\rm{ }} + {\rm{ }}{m^2} = {\rm{ }}0\) có nghiệm khi
\(\Delta '{\rm{ }} = {\rm{ }}{m^{2}} - {\rm{ }}2m{\rm{ }} + {\rm{ }}1{\rm{ }}-{\rm{ }}{m^2} = {\rm{ }}1{\rm{ }}-{\rm{ }}2m{\rm{ }} \ge {\rm{ }}0\)
hay khi \(m ≤\) \(\frac{1}{2}\)
Khi đó \({x_{1}} + {\rm{ }}{x_2} = {\rm{ }}2\left( {m{\rm{ }}-{\rm{ }}1} \right)\), \({\rm{ }}{x_{1}}.{\rm{ }}{x_2} = {\rm{ }}{m^2}\)