\(\sqrt{2x^2}\)
ĐKXĐ: \(2x^2\ge0\left(đúng\forall x\right)\)
Vậy \(x\in R\)
\(\sqrt{2x^2}\)
ĐKXĐ: \(2x^2\ge0\left(đúng\forall x\right)\)
Vậy \(x\in R\)
Điều kiện xác định của biểu thức \(\sqrt{\dfrac{1}{x^2-2x+1}}\)
Tìm điều kiện xác định và rút gọn
\(P=\left(\dfrac{\sqrt{x}}{\sqrt{x-1}}-\dfrac{1}{x-\sqrt{x}}\right):\left(\dfrac{1}{1+\sqrt{x}}+\dfrac{2}{x-1}\right)\)
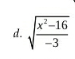 (tìm điều kiện xác định)
(tìm điều kiện xác định)
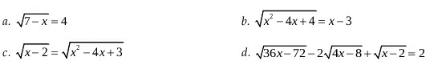 ( tìm x biết)
( tìm x biết)
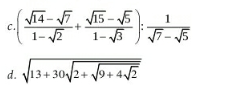 (rút gọn)
(rút gọn)
Các anh e giúp mik vs
Cho biểu thức A=(\(\dfrac{x\sqrt{x}-1}{x-\sqrt{x}}-\dfrac{x\sqrt{x}+1}{x+\sqrt{x}}\)) : (\(1-\dfrac{3-\sqrt{x}}{\sqrt{x}+1x}\))
1.Tìm điều kiện xác định của biểu thức A.
2.Rút gọn A.
3.Tính giá trị biểu thức A khi x = \(\dfrac{1}{6-2\sqrt{5}}\).
4.Tìm giá trị nguyên của x để biểu thức A nhận giá trị nguyên.
5.Tìm giá trị của x để biểu thức A bằng -3.
6.Tìm giá trị của x để biểu thức A nhỏ hơn -1.
7.Tìm giá trị của x để biểu thức A lớn hơn \(\dfrac{-2}{\sqrt{x}+1}\)
tìm điều kiện xác định
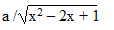
Tìm điều kiện xác định
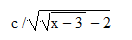
Tìm đièu kiện xác định của bth sau:
\(\left(\dfrac{3\sqrt{x}}{x-4}-\dfrac{3}{\sqrt{x}-2}\right).\dfrac{\sqrt{x}-2}{x-4}\)
A=\(\left(\dfrac{1}{1-X}=\dfrac{1}{\sqrt{X+1}}\right)^2\cdot\dfrac{X^2-1}{2}-\sqrt{1-X^2}\)
1) Tìm điều kiện của x để A được xác định
2) rút gọn biểu thức A
3) tìm x khi A=-2
Cho mìh hỏi cách tìm điều kiện xác định thì mìh tìm như thế nào ạ