Bài 8: Các trường hợp đồng dạng của tam giác vuông
Các câu hỏi tương tự
Cho tam giác ABC vuông tại A, chân H của đường cao AH chia cạnh huyền BC thành hai đoạn có độ dài 4cm và 9 cm
Gọi D và E là hình chiếu của H trên AB và AC
a) Tính độ dài DE
b) Các đường thẳng vuông góc với DE tại D và E cắt BC theo thứ tự tại M và N. Chứng minh M là trung điểm của BF, N là trung điểm của CH
c) Tính diện tích tứ giác DENM
Bài1. Cho tam giác ABC vuông tại A. Kẻ đường cao AH (H thuộc BC).
a) Tìm các cặp tam giác đồng dạng.
b) Chứng minh AH2=BH.CH; AB2 = BH.BC; AC2 = CH.BC
c) Biết BH=9cm, CH = 16cm. Tính độ dài các cạnh của tam giác ABC.
Chân đường cao AH của tam giác vuông ABC chia cạnh huyền BC thành 2 đoạn thẳng có độ dài 25 cm và 36 cm. Tính chu vi và diện tích của tam giác vuông đó (h.53)
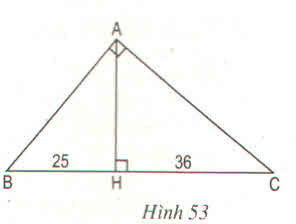
Hướng dẫn : Trước tiên tìm cách tính AH từ các tam giác vuông đồng dạng, sau đó tính các cạnh của tam giác BC
Cho tam giác ABC vuông tại A
Có AB=15cm,AC=20cm
Kẻ đường cao AH,phân bức AD(H và D thuộcBC)
a)CM tam giác ABH và ABC đồng dạng
b tính đọ dài BC BD AH
c)Trên tia đối của DA lấy điển I sao cho góc ACI=ABC tính diện tích tam giác AIC
Mn giúp mik vs ạ
Mik đang cần gấp
Xem chi tiết
Cho Tam giác ABC vuông tại A có AB=9cm, AC=12cm , đường cao AH a) chứng minh: tam giác abh ~ tam giác cba b) tính BC;AH c) Tia phân giác góc B cắt AC tại D.Chứng minh: AD.AC=AH.DC
Đường cao của một tam giác vuông xuất phát từ đỉnh góc vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 9cm và 16 cm.
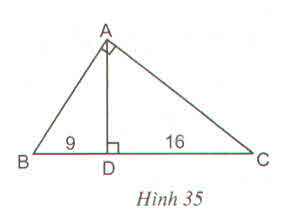
Tính độ dài các cạnh của tam giác vuông đó (h.35) ?
Cho tam giác ABC vuông tại A ( AC > AB ), đường cao AH. Trên tia HC lấy điểm D sao cho HD = AH. Qua D kẻ đường thẳng vuông góc với BC, cắt cạnh AC tại E.
a) Chứng minh tam giác ABC đồng dạng với tam giác HAC
b) Chứng minh EC . AC = DC. BC
c) Chứng minh tam giác BEC = tam giác ADC và tam giác ABE vuông cân
cho tam giác ABC vuông tại A,đường cao AH.
a. CM tam giác ABH đồng dạng với tam giác CBA
b.Gọi E là điểm tùy ý trên cạnh AB, ĐƯờng thẳng đi qua H và vuông góc với HEcawts AC tại F. Tìm vị trí của điểm E trên cạnh AB để tam giác EHFcó diện tích nhỏ nhất
Cho tam giác ABC vuông tại A có AB bằng 6 cm,AC bằng 8 cm.Vẽ đường cao AH.Chứng minh:
a)tam giác HCA đồng dạng với tam giác ACB
b)Tính BC,AH,CH,BH
c)Vẽ đường phân giác AD của tam giác ABC Tính BD,CD
d)Trên AH lấy điểm K sao cho AK bằng 3,6 cm .Từ K kẻ đường thẳng song song với BC cắt AB và AC lần lượt tại M và N.Tính diện tích tứ giác BMNC
đ) Trong tam giác ADB kẻ đường phân giác DE , trong tam giác ADC kẻ đường phân giác DF
Cm:EA/EB.DB/DC.FC/FA1(Hay EA.DB.FCEB.DC.FA)
Đọc tiếp
Cho tam giác ABC vuông tại A có AB bằng 6 cm,AC bằng 8 cm.Vẽ đường cao AH.Chứng minh: a)tam giác HCA đồng dạng với tam giác ACB b)Tính BC,AH,CH,BH c)Vẽ đường phân giác AD của tam giác ABC Tính BD,CD d)Trên AH lấy điểm K sao cho AK bằng 3,6 cm .Từ K kẻ đường thẳng song song với BC cắt AB và AC lần lượt tại M và N.Tính diện tích tứ giác BMNC đ) Trong tam giác ADB kẻ đường phân giác DE , trong tam giác ADC kẻ đường phân giác DF Cm:EA/EB.DB/DC.FC/FA=1(Hay EA.DB.FC=EB.DC.FA)










