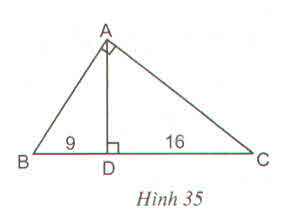
\(AB^2 + AC^2 = 25^2 = 625\)
\(AD^2 + 81 = AB^2\)
\(AD^2 + 256 = AC^2\)
\(=> AD^2 + 81 + AD^2 + 256 = 625\)
=> \(2AD^2 = 288\)
=> \(AD^2 = 144\)
=> AD = 12(cm)
=>\( AB^2 = 9^2 + 12^2 = 225\)
=> AB = 15 (cm)
=> \(AC^2 = 12^2 + 16^2 = 400\)
=> AC = 20(cm)
và BC = 25(cm)

Ta có: \(BC=BD+DC=9+16=25\left(cm\right)\)
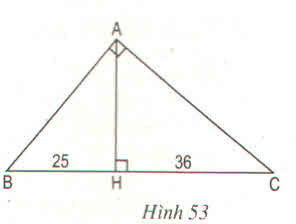
Xét \(\Delta DBA\) và \(\Delta ABC\):
\(\widehat{A}=\widehat{D}\left(=90^o\right)\)
\(\widehat{B}=\widehat{A_2}\)(cùng phụ với góc\(A_1\))
\(\Rightarrow\Delta DBA\)~\(\Delta ABC\)
\(\Rightarrow\dfrac{DB}{AB}=\dfrac{AB}{BC}\Leftrightarrow AB^2=DB.BC=9.25=225\Rightarrow AB=15\left(cm\right)\)
Áp dụng định lý Py-ta-go cho tam giác vuông ABC, có:
\(AB^2+AC^2=BC^2\Leftrightarrow15^2+AC^2=25^2\Rightarrow AC=\sqrt{25^2-15^2}=20\)
Vậy các cạnh của tam giác vuông ABC lần lượt là: \(15;20;25\)
AB2 + AC2 = 252 = 625
AD2 + 81 = AB2
AD2 + 256 = AC2
=> AD2 + 81 + AD2 + 256 = 625
=> 2AD2 = 288
=> AD2 = 144
=> AD = 12(cm)
=> AB2 = 92 + 122 = 225
=> AB = 15 (cm)
=> AC2 = 122 + 162 = 400
=> AC = 20(cm)
và BC = 25(cm)
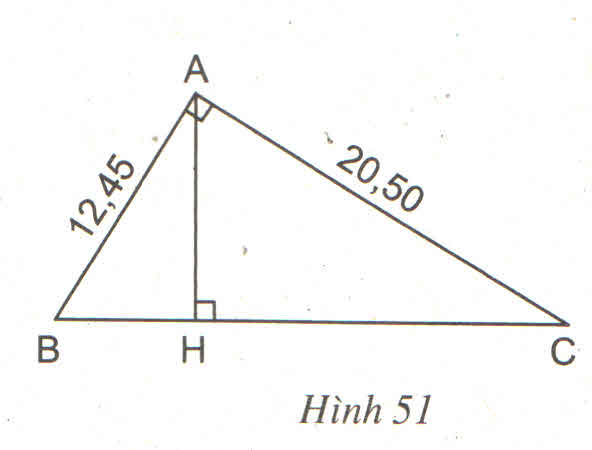
Xét 2 tg vuông HBA và HAC có:
gBAH + gHAC = 90 độ
gHCA + gHAC = 90 độ
=> gBAH = gHCA
và tg HBA ~ tg HAC
=> \(\dfrac{BH}{AH}=\dfrac{AH}{CH}\Rightarrow AH^2=BH.CH=9.16=144\)
=> AH = \(\sqrt{144}=12cm\)
Áp dụng định lý py - ta - go ta có:
\(BC=BH+CH=9+16=25cm\)
\(AB^2=HB^2+HA^2=9^2+12^2=225\Rightarrow AB=\sqrt{225}=15cm\)
\(AC^2=HC^2+HA^2=16^2+12^2=400\Rightarrow AB=\sqrt{400}=20cm\)
\(\)