Question

Tam giác ABC có AB=8cm, AC=15cm, BC=17cm, đương cao AH. Tính độ dài AH

Answer 1

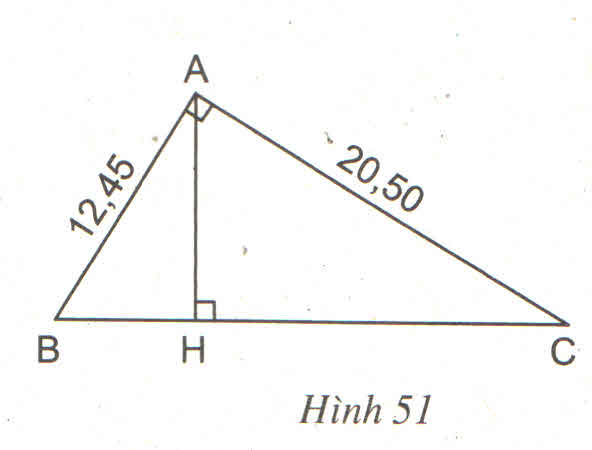
Ta có: AB² + AC² = 8² + 5² =289

BC² =17² = 289

\(\Rightarrow\)BC² = AB² + AC²

\(\Rightarrow\)\(\Delta\) ABC vuông tại A.

Xét \(\Delta\) ABC và \(\Delta\) HBA ta có:

\(\Lambda\) BAC = \(\Lambda\) BHA ( AB\(\perp\)AC, AH\(\perp\)BC)

và \(\Lambda\)B là góc chung

\(\Rightarrow\)\(\Delta\)ABC ~ \(\Delta HBA\)(g.g)

\(\Rightarrow\dfrac{AC}{BC}=\dfrac{HA}{BA}\)

\(\Rightarrow\dfrac{15}{17}=\dfrac{HA}{8}\)

\(\Rightarrow HA=\dfrac{15}{17}\times8=\dfrac{120}{17}\)

Vậy AH = \(\dfrac{120}{17}\)

Answer 2