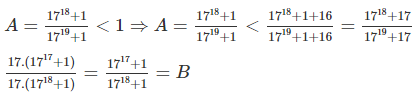Bài này có rất nhiều cách lm nhé!
Ta có : A = \(\dfrac{17^{18}+1}{17^{19}+1}\) => 17A = \(\dfrac{17^{19}+17}{17^{19}+1}\) = \(1+\dfrac{16}{17^{19}+1}\)
B = \(\dfrac{17^{17}+1}{17^{18}+1}\) => 17B = \(\dfrac{17^{18}+17}{17^{18}+1}\) = \(1+\dfrac{16}{17^{18}+1}\)
Vì \(\dfrac{16}{17^{19}+1}\) < \(\dfrac{16}{17^{18}+1}\) ( vì 1719 +1 > 1716+1 )
=> \(1+\dfrac{16}{17^{19}+1}\) < \(1+\dfrac{16}{17^{18}+1}\)
=> 17A < 17B
=> A < B ( vì 17 > 0)
Ta có :
\(A=\dfrac{17^{18}+1}{17^{19}+1}\)
17A= \(17\times\dfrac{17^{18}+1}{17^{19}+1}\)
\(17A=\dfrac{17^{19}+17}{17^{19}+1}\)
\(17A=\dfrac{\left(17^{19}+1\right)+16}{17^{19}+1}\)
\(17A=\dfrac{17^{19}+1}{17^{19}+1}+\dfrac{16}{17^{19}+1}\)
\(17A=1+\dfrac{16}{17^{19}+1}\)
Lại có :
\(B=\dfrac{17^{17}+1}{17^{18}+1}\)
\(17B=17\times\dfrac{17^{17}+1}{17^{18}+1}\)
\(17B=\dfrac{17^{18}+17}{17^{18}+1}\)
\(17B=\dfrac{\left(17^{18}+1\right)+16}{17^{18}+1}\)
\(17B=\dfrac{17^{18}+1}{17^{18}+1}+\dfrac{16}{17^{18}+1}\)
\(17B=1+\dfrac{16}{17^{18}+1}\)
Mà : \(\dfrac{16}{17^{19}+1}< \dfrac{16}{17^{18}+1}\)
\(\Rightarrow1+\dfrac{16}{17^{19}+1}< 1+\dfrac{16}{17^{18}+1}\)
⇒ A < B
Vậy A < B
Giải : Vì A= \(\)\(\dfrac{17^{18}+1}{17^{19}+1}\) <1 nên áp dụng tính chất . Nếu \(\dfrac{a}{b}\) < 1 thì \(\dfrac{a}{b}\) < \(\dfrac{a+m}{b+m}\) ( a ϵ N , b ϵ N✳ ) Ta có : A= \(\dfrac{17^{18}+1}{17^{19}+1}\)< \(\dfrac{17^{18}+1+16}{17^{19}+1+16}\) =\(\dfrac{17^{18}+17}{17^{19}+17}\) =\(\dfrac{17.17^{17}+17.1}{17.17^{18}+17.1}\)=\(\dfrac{17.\left(17^{17}+1\right)}{17.\left(17^{18}+1\right)}\) =\(\dfrac{17^{17}+1}{17^{18}+1}\) = B ⇔ A<B
17A= \(\dfrac{17^{19}+1+16}{17^{19}+1}\)
17A=1\(\dfrac{16}{17^{19}+1}\)
Ta có:
17B=\(\dfrac{17^{18}+1+16}{17^{18}+1}\)
17B=1\(\dfrac{16}{17^{18}+1}\)
Mà 1\(\dfrac{16}{17^{19}+1}\)<1\(\dfrac{16}{17^{18}+1}\)
⇒17A>17B
Vậy A>B