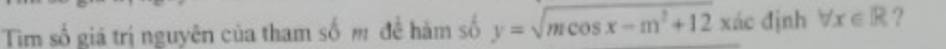1.
\(sin^3x+cos^3x\le sin^2x+cos^2x=1\)
\(2-sin^4x\ge1\Leftrightarrow sin^4x\le1\)
\(\Rightarrow sin^3x+cos^3x\le2-sin^4x\)
Đẳng thức xảy ra khi:
\(\left\{{}\begin{matrix}sin^3x+cos^3x=1\\sin^4x=1\end{matrix}\right.\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)
2.
\(\left(sinx+\sqrt{3}cosx\right)sin3x=2\)
\(\Leftrightarrow\left(\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx\right)sin3x=1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{3}\right)sin3x=1\)
\(\Leftrightarrow cos\left(2x-\dfrac{\pi}{3}\right)-cos\left(4x+\dfrac{\pi}{3}\right)=2\)
Ta có:
\(cos\left(4x+\dfrac{\pi}{3}\right)\ge-1\Rightarrow-cos\left(4x+\dfrac{\pi}{3}\right)\le1\)
\(cos\left(2x-\dfrac{\pi}{3}\right)\le1\)
\(\Rightarrow cos\left(2x-\dfrac{\pi}{3}\right)-cos\left(4x+\dfrac{\pi}{3}\right)\le1-\left(-1\right)=2\)
Đẳng thức xảy ra khi:
\(\left\{{}\begin{matrix}cos\left(2x-\dfrac{\pi}{3}\right)=1\\cos\left(4x+\dfrac{\pi}{3}\right)=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-\dfrac{\pi}{3}=k2\pi\\4x+\dfrac{\pi}{3}=\pi+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
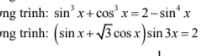
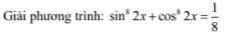
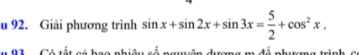
mọi người giải giúp em theo phương pháp tự luận với ạ 
