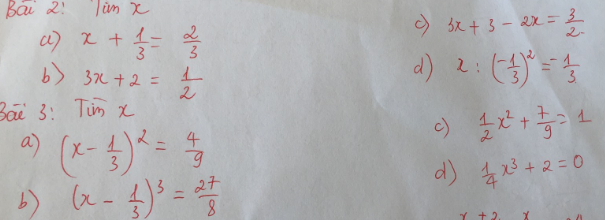a. \(a\left(a-1\right)-\left(a+3\right)\left(a+2\right)=a^2-a-\left(a^2+5a+6\right)=-6a-6=6\left(-a-1\right)⋮6\)
b. \(a\left(a+2\right)-\left(a-5\right)\left(a-7\right)=a^2+2a-\left(a^2-12a+35\right)=14a-35=7\left(2a-5\right)⋮7\)
c. \(\left(n^2-3n+1\right)\left(n+2\right)-n^3+n^2+3=n^3-n^2-5n+2-n^3+n^2+3=-5n+5\)
\(=5\left(1-n\right)⋮5\)
a) \(a\left(a-1\right)-\left(a+3\right)\left(a+2\right)=a^2-a-a^2-5a-6=-6a-6=-6\left(a+1\right)⋮6,\forall a\in Z\)
b) \(a\left(a+2\right)-\left(a-5\right)\left(a-7\right)=a^2+2a-a^2+12a-35=14a-35=7\left(2a-5\right)⋮7,\forall a\in Z\)c) \(\left(n^2-3n+1\right)\left(n+2\right)-n^3+n^2+3=n^3-n^2-5n+2-n^3+n^2+3=-5n+5=-5\left(n-5\right)⋮5,\forall n\in Z\)
a: Ta có: \(a\left(a-1\right)-\left(a+3\right)\left(a+2\right)\)
\(=a^2-a-a^2-5a-6\)
\(=-6a-6⋮6\)
b: Ta có: \(a\left(a+2\right)-\left(a-5\right)\left(a-7\right)\)
\(=a^2+2a-a^2+12a-35\)
\(=14a-35⋮7\)
c: Ta có: \(\left(n^2-3n+1\right)\left(n+2\right)-n^3+n^2+3\)
\(=n^3+2n^2-3n^2-6n+n+2-n^3+n^2+3\)
\(=-5n+5⋮5\)

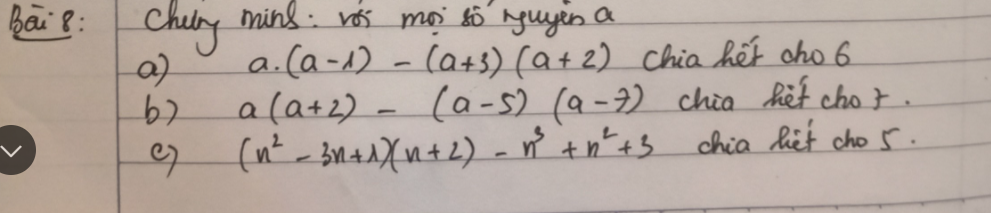








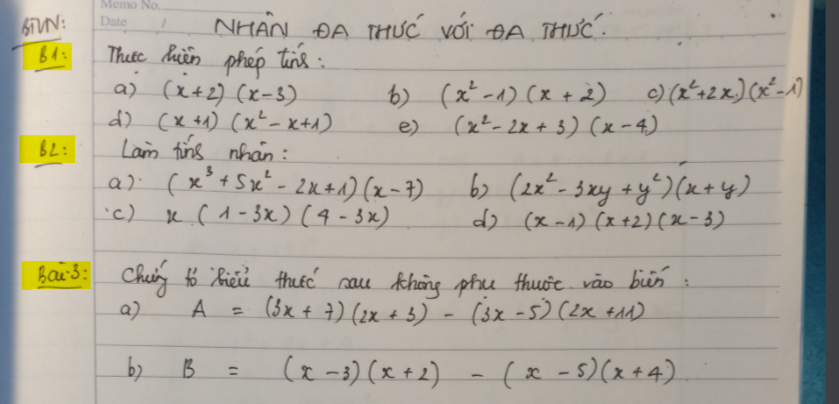





 mn lm giúp mik vs ạ.Mik đang cần gấp ạ.Nhanh ạ
mn lm giúp mik vs ạ.Mik đang cần gấp ạ.Nhanh ạ