a/ ĐKXĐ: \(x\ge-\dfrac{3}{2}\)
\(\sqrt{2x+3}=1+\sqrt{2}\)
\(\Leftrightarrow2x+3=1+2\sqrt{2}+2\)
\(\Leftrightarrow2x=2\sqrt{2}\)
\(\Leftrightarrow x=\sqrt{2}\) ( tmđk)
Vậy phương trình có nghiệm \(x=\sqrt{2}\)
b/ ĐKXĐ: \(x\ge-\dfrac{10}{\sqrt{3}}\)
\(\sqrt{10+\sqrt{3}x}=2+\sqrt{6}\)
\(\Leftrightarrow10+\sqrt{3}x=4+4\sqrt{6}+6\)
\(\Leftrightarrow\sqrt{3}x=4\sqrt{6}\)
\(\Leftrightarrow x=4\sqrt{2}\) ( tmđk)
Vậy phương trình có nghiệm \(x=4\sqrt{2}\)
c/ \(x\ge\dfrac{2}{3}\)
\(\sqrt{3x-2}=2-\sqrt{3}\)
\(\Leftrightarrow3x-2=4-4\sqrt{3}+3\)
\(\Leftrightarrow3x=9-4\sqrt{3}\)
\(\Leftrightarrow x=\dfrac{9-4\sqrt{3}}{3}\) ( tmđk)
Vậy phương trình có nghiệm \(x=\dfrac{9-4\sqrt{3}}{3}\)
d/ Xét vế trái phương trình: \(\sqrt{x+1}\ge0\) (1)
vế phải phương trình: \(\sqrt{5}-3< 0\left(2\right)\)
Ta thấy (1) và (2) mâu thuẫn \(\Rightarrow\) Phương trình đã cho vô nghiệm
a) \(\sqrt{2x+3}\)= 1 + \(\sqrt{2}\)( ĐK : x \(\ge\dfrac{-3}{2}\))
<=> 2x + 3 = ( 1 + \(\sqrt{2}\))2
<=> 2x + 3 = 1 + 2\(\sqrt{2}\)+2
<=> 2x = 2\(\sqrt{2}\)
<=> x = \(\sqrt{2}\)( TMĐK )
Vậy x = \(\sqrt{2}\)






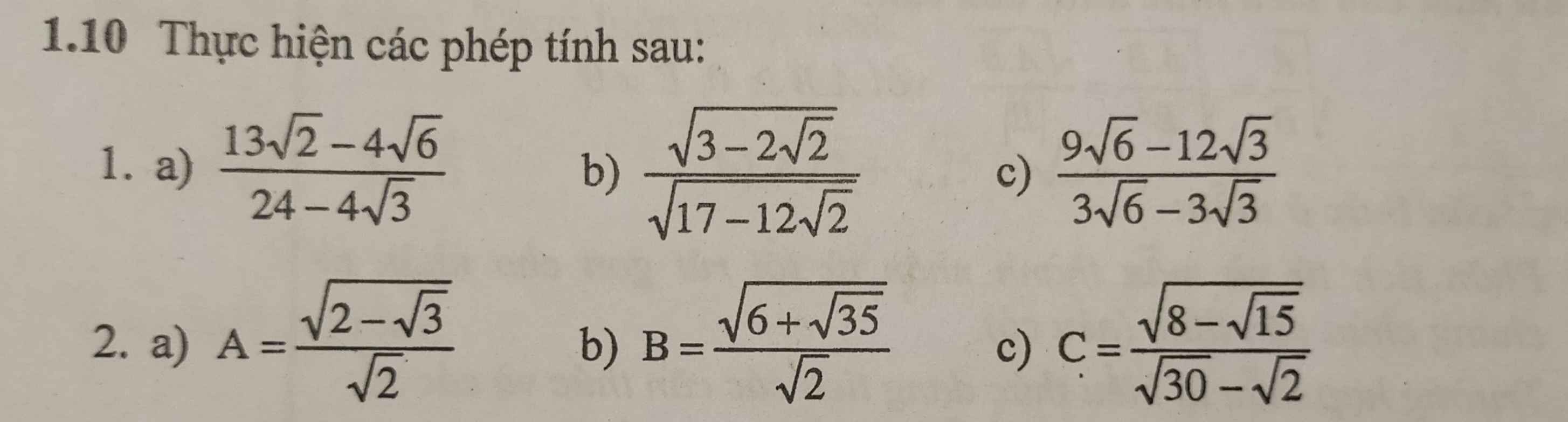





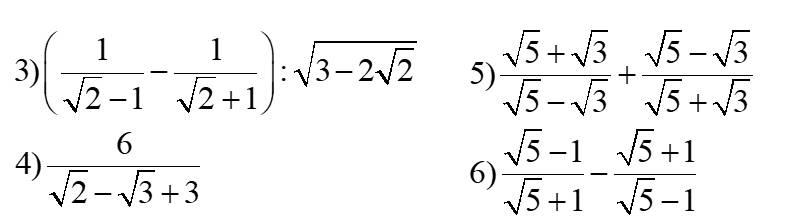

 giúp mình câu 11 , 12 v ạ mình camon
giúp mình câu 11 , 12 v ạ mình camon