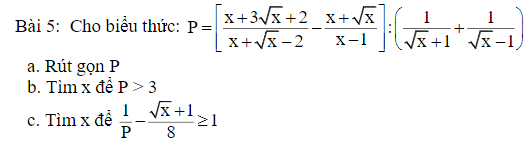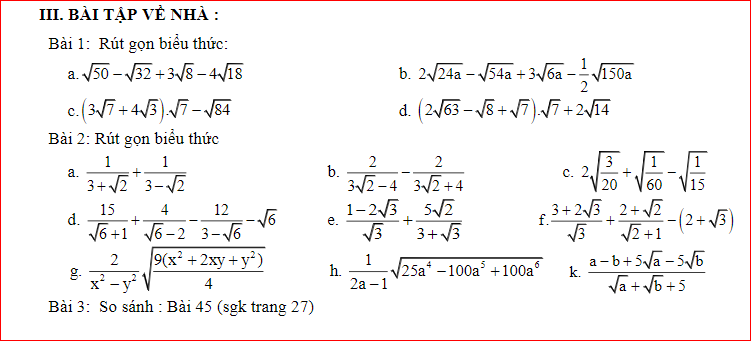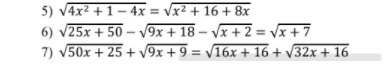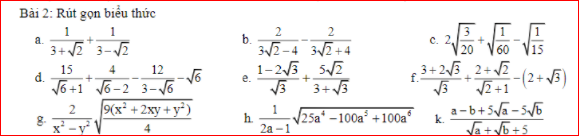\(a,P=\left[\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right]:\dfrac{\sqrt{x}-1+\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\\ P=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}}{\sqrt{x}-1}\right):\dfrac{2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ P=\dfrac{\sqrt{x}+1-\sqrt{x}}{\sqrt{x}-1}\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{2\sqrt{x}}\\ P=\dfrac{\sqrt{x}+1}{2\sqrt{x}}\\ b,P>3\left(x>0;x\ne1\right)\Leftrightarrow\dfrac{\sqrt{x}+1}{2\sqrt{x}}-3>0\\ \Leftrightarrow\dfrac{\sqrt{x}+1-6\sqrt{x}}{2\sqrt{x}}>0\\ \Leftrightarrow1-5\sqrt{x}>0\left(2\sqrt{x}>0\right)\\ \Leftrightarrow\sqrt{x}< \dfrac{1}{5}\Leftrightarrow0\le x< \dfrac{1}{25}\)
\(c,\dfrac{1}{P}-\dfrac{\sqrt{x}+1}{8}\ge1\\ \Leftrightarrow\dfrac{2\sqrt{x}}{\sqrt{x}+1}-\dfrac{\sqrt{x}+1}{8}-1\ge0\\ \Leftrightarrow\dfrac{16\sqrt{x}-x-2\sqrt{x}-1-8}{8\left(\sqrt{x}+1\right)}\ge0\\ \Leftrightarrow-x+14\sqrt{x}-9\ge0\\ \Leftrightarrow7-2\sqrt{10}\le\sqrt{x}\le7+2\sqrt{10}\\ \Leftrightarrow89-28\sqrt{10}\le x\le89+28\sqrt{10}\)