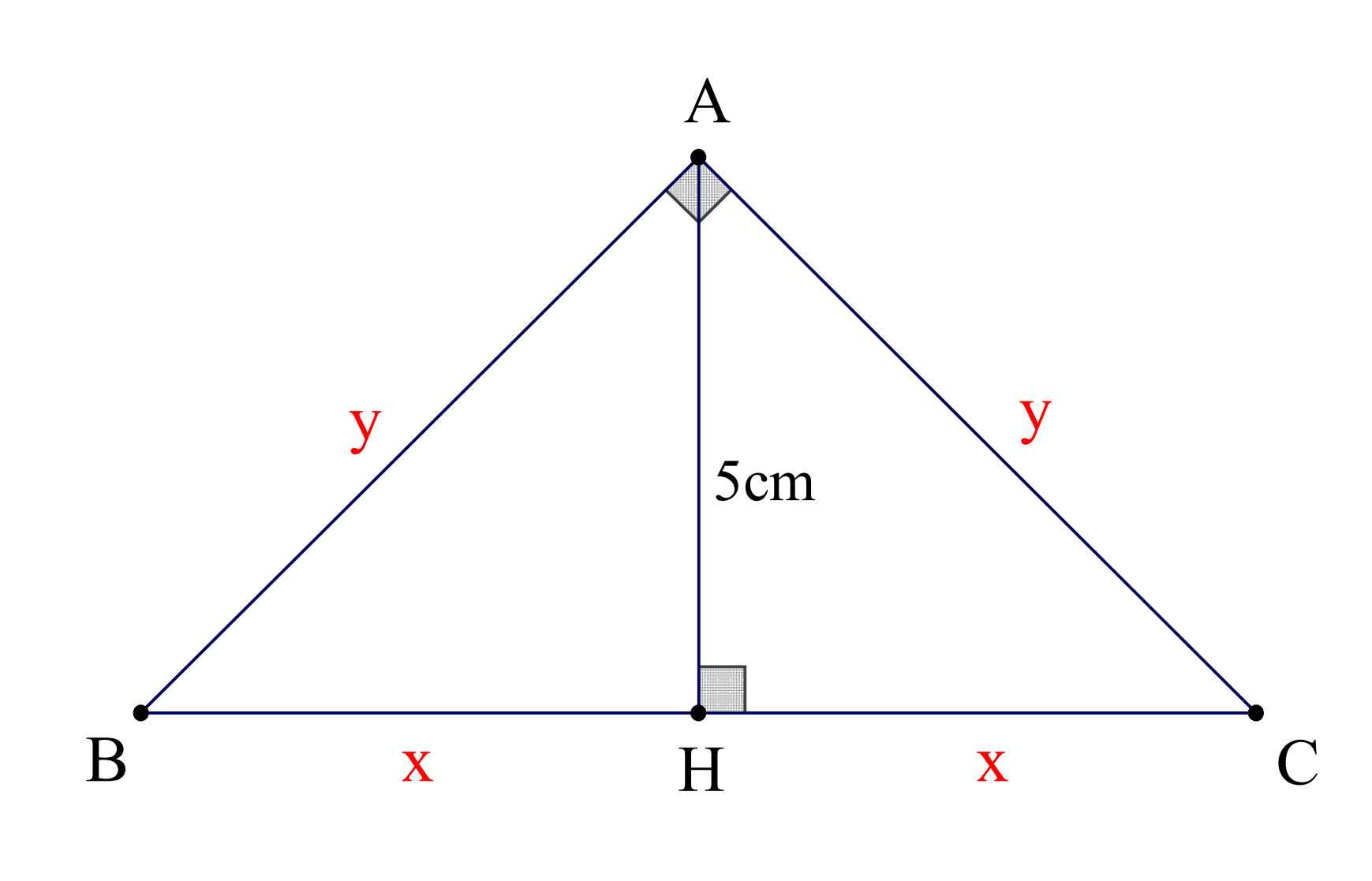
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=5^2+12^2=169\)
=>BC=13
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\BH\cdot BC=BA^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AH=\dfrac{5\cdot12}{13}=\dfrac{60}{13}\left(cm\right)\\BH=\dfrac{5^2}{13}=\dfrac{25}{13}\left(cm\right)\end{matrix}\right.\)
b: Xét ΔABE vuông tại A có AI là đường cao
nên \(BI\cdot BE=BA^2\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BA^2=BH\cdot BC\)
=>\(BI\cdot BE=BH\cdot BC=2\cdot BH\cdot BM\)
c: