\(a,A\left(x\right)=x^2+3x^4-4x+7+x^4\)
\(=x^2+4x^4-4x+7\)
Sắp xếp : \(4x^4+x^2-4x+7\)
\(B\left(x\right)=x^4-2x^2+\left(1-5x^4+4x-4\right)\)
\(=x^4-2x^2+1-5x^4+4x-4\)
\(=-4x^4-2x^2+4x-3\) ( Đã sắp xếp )
\(b,\) \(C\left(x\right)-A\left(x\right)=B\left(x\right)\)
\(\Rightarrow C\left(x\right)=A\left(x\right)+B\left(x\right)\)
\(=4x^4+x^2-4x+7-4x^4-2x^2+4x-3\)
\(=-x^2+4\)
Đặt \(C\left(x\right)=0\Rightarrow-x^2+4=0\Rightarrow x^2=-4\left(ktm\right)\)
Vậy C(x) vô nghiệm

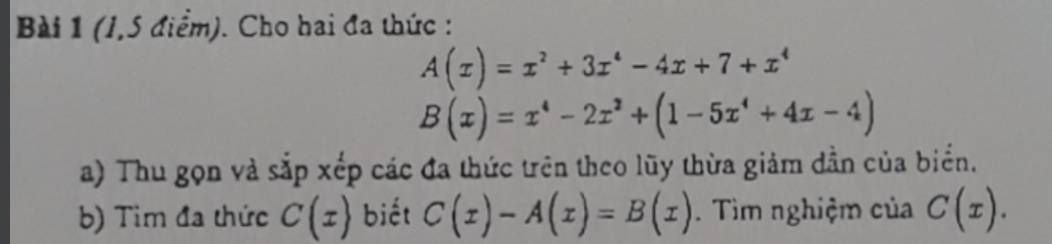




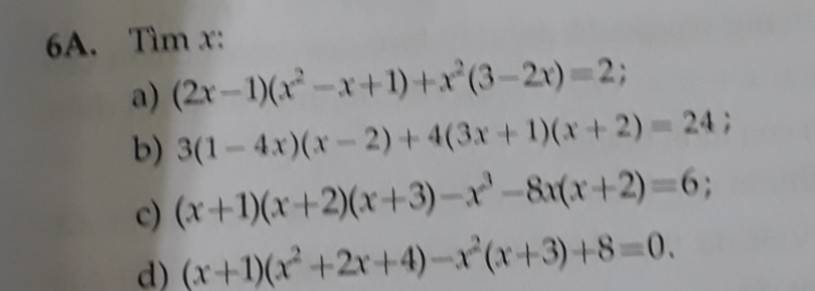 giúp em làm vs ạ
giúp em làm vs ạ



 giúp em vs ạ
giúp em vs ạ



