6 cặp lá mầm gợi nên những hình đồng dạng là:
- Lá 1 và 3
- Lá 3 và 5
- Lá 1 và 5
- Lá 2 và 4
- Lá 4 và 6
- Lá 2 và 6
6 cặp lá mầm gợi nên những hình đồng dạng là:
- Lá 1 và 3
- Lá 3 và 5
- Lá 1 và 5
- Lá 2 và 4
- Lá 4 và 6
- Lá 2 và 6
Cho tam giác ABC đồng dạng với tam giác A'B'C' theo tỉ số đồng dạng \(k\).
a) Cho AM, A'M' lần lượt là các đường trung tuyến của các tam giác ABC, A'B'C'. Chứng minh \(\Delta ABM \backsim \Delta A'B'M'\) và \(\frac{{AM}}{{A'M'}} = k\).
b) Cho AD, A'D' lần lượt là các đường phân giác của các tam giác ABC, A'B'C'. Chứng minh \(\Delta ABD \backsim \Delta A'B'D'\) và \(\frac{{AD}}{{A'D'}} = k\).
c) Cho AH, A'H' lần lượt là các đường cao của các tam giác ABC, A'B'C'. Chứng minh \(\Delta ABH \backsim \Delta A'B'H'\) và \(\frac{{AH}}{{A'H'}} = k\).
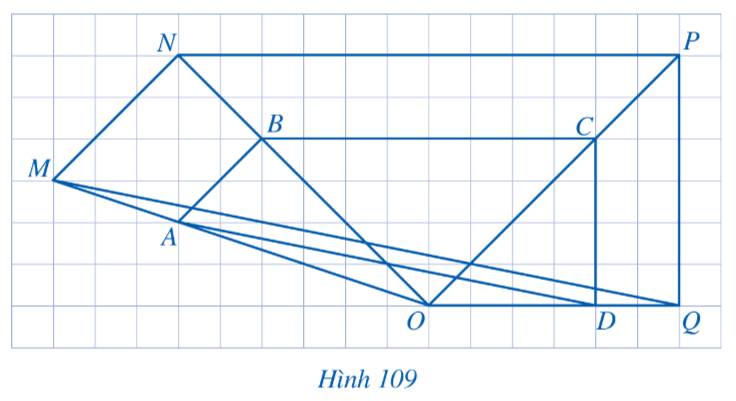
Cho Hình 109. Hình nào đồng dạng phối cảnh với:
a) Tam giác OAB?
b) Tam giác OBC?
c) Tam giác OCD?
d) Tứ giác ABCD?
Cho hình bình hành ABCD. Gọi M, N, P lần lượt là trung điểm của các đoạn thẳng AB, BC, AN và Q là giao điểm của AN và DM. Chứng minh:
a) \(MP\parallel AD,\,\,MP = \frac{1}{4}AD\)
b) \(AQ = \frac{2}{5}AN\)
c) Gọi R là trung điểm của CD. Chứng minh ba điểm M, P, R thẳng hàng và \(PR = \frac{3}{4}AD\).
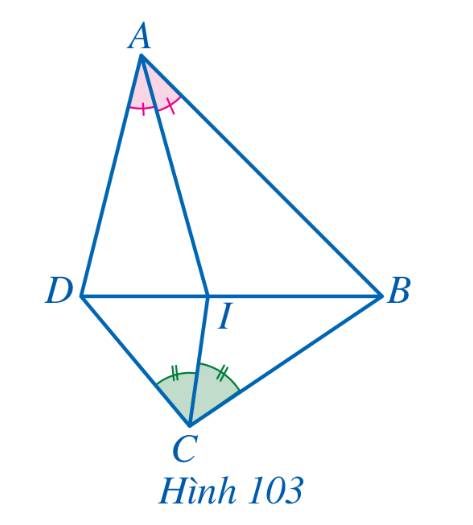
Cho tứ giác ABCD. Tia phân giác của các góc BAD và BCD cắt nhau tại điểm I. Biết I thuộc đoạn thẳng BD (Hình 103). Chứng minh \(AB.CD = AD.BC\).
Cho tam giác ABC có M, N là hai điểm lần lượt thuộc các cạnh AB, AC sao cho \(MN\parallel BC\). Gọi I, P, Q lần lượt là giao điểm của BN và CM, AI và MN, AI và BC. Chứng minh:
a) \(\frac{{MP}}{{BQ}} = \frac{{PN}}{{QC}} = \frac{{AP}}{{AQ}}\)
b) \(\frac{{MP}}{{QC}} = \frac{{PN}}{{BQ}} = \frac{{IP}}{{IQ}}\)
Cho \(\Delta DEG \backsim \Delta MNP,\,\,\widehat E = 60^\circ ,\,\,\widehat M = 40^\circ \).
a) Số đo góc D bằng bao nhiêu độ?
A. \(40^\circ \)
B. \(50^\circ \)
C. \(60^\circ \)
D. \(80^\circ \)
b) Số đo góc N bằng bao nhiêu độ?
A. \(40^\circ \)
B. \(50^\circ \)
C. \(60^\circ \)
D. \(80^\circ \)
b) Số đo góc P bằng bao nhiêu độ?
A. \(40^\circ \)
B. \(50^\circ \)
C. \(60^\circ \)
D. \(80^\circ \)
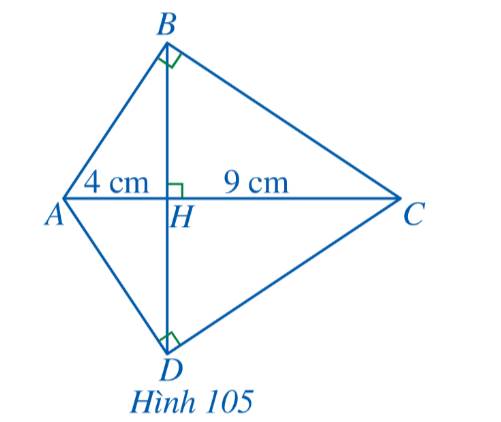
Cho Hình 105. Chứng minh:
a) \(\Delta HAB \backsim \Delta HBC\)
b) \(HB = HD = 6cm\)
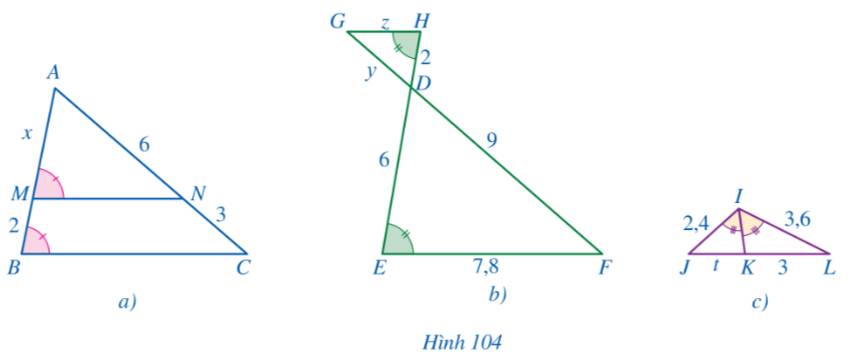
Tính các độ dài x, y, z, t ở các hình 104a, 104b, 104c.
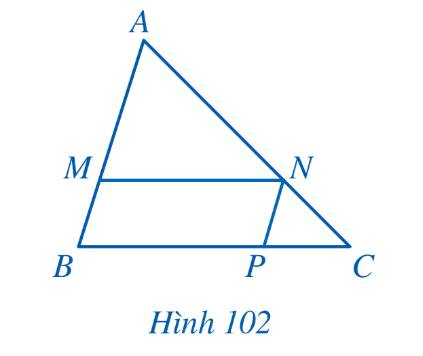
Cho tam giác ABC, các điểm M, N, P lần lượt thuộc các cạnh AB, AC, BC sao cho tứ giác BMNP là hình bình hành (Hình 102). Chứng minh \(\frac{{MN}}{{BC}} + \frac{{NP}}{{AB}} = 1\).