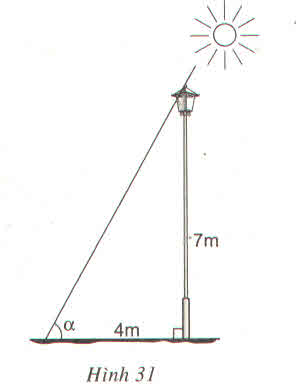
1:
ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot5=3\cdot4=12\)
=>AH=2,4(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{3^2}{5}=1.8\left(cm\right)\\CH=\dfrac{4^2}{5}=3.2\left(cm\right)\end{matrix}\right.\)
2:
Chúng ta sẽ gọi AB,AC là hai cạnh góc vuông
AH,AM lần lượt là đường cao và đường trung tuyến kẻ từ A xuống cạnh huyền BC
Theo đề, ta có: AH=4cm và AM=5cm
ΔABC vuông tại A có AM là trung tuyến
nên BC=2*AM
=>BC=10(cm)
Đặt HB=x; HC=y
HB+HC=BC
=>x+y=10(1)
Xét ΔABC vuông tại A có AH là đường cao
nên \(HB\cdot HC=AH^2\)
=>\(x\cdot y=4^2=16\)(2)
Từ (1), (2) suy ra x,y là các nghiệm của phương trình:
\(a^2-10a+16=0\)
=>(a-2)(a-8)=0
=>\(\left[{}\begin{matrix}a=2\\a=8\end{matrix}\right.\)
TH1: \(\left\{{}\begin{matrix}BH=2cm\\CH=8cm\end{matrix}\right.\)
\(AB=\sqrt{BH\cdot BC}=\sqrt{20}=2\sqrt{5}\left(cm\right)\)
\(AC=\sqrt{CH\cdot CB}=\sqrt{8\cdot10}=\sqrt{80}=4\sqrt{5}\left(cm\right)\)
TH2: \(\left\{{}\begin{matrix}BH=8cm\\CH=2cm\end{matrix}\right.\)
\(AB=\sqrt{BH\cdot BC}=4\sqrt{5}\left(cm\right)\)
\(AC=\sqrt{CH\cdot CB}=2\sqrt{5}\left(cm\right)\)

 help tui giải đi mà
help tui giải đi mà







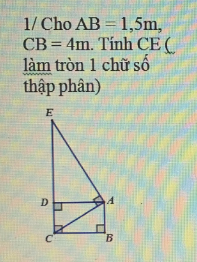 giải giúp mình vớii
giải giúp mình vớii