\(\left(x+1\right)\left(x-2\right)< 0\)
\(\Rightarrow\left[{}\begin{matrix}x+1< 0\\x-2< 0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x< -1\\x< 2\end{matrix}\right.\)
\(\left(x-2\right)\left(x+\dfrac{2}{3}\right)>0\)
\(\Rightarrow\left[{}\begin{matrix}x-2>0\\x+\dfrac{2}{3}>0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x>2\\x>-\dfrac{2}{3}\end{matrix}\right.\)
a) \(\left(x+1\right)\left(x-2\right)< 0\)
\(\Rightarrow\left\{{}\begin{matrix}x+1>0\\x-2< 0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x>-1\\x< 2\end{matrix}\right.\)\(\Rightarrow2>x>-1\)
\(\Rightarrow\left\{{}\begin{matrix}x+1< 0\\x-2>0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x< -1\\x>2\end{matrix}\right.\)=> VN
b) \(\left(x-2\right)\left(x+\dfrac{2}{3}\right)>0\)
\(\Rightarrow\left\{{}\begin{matrix}x-2>0\\x+\dfrac{2}{3}>0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x>2\\x>-\dfrac{2}{3}\end{matrix}\right.\)\(\Rightarrow x>2\)
\(\Rightarrow\left\{{}\begin{matrix}x-2< 0\\x+\dfrac{2}{3}< 0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x< 2\\x< -\dfrac{2}{3}\end{matrix}\right.\)\(\Rightarrow x< -\dfrac{2}{3}\)
a)
Có:(x+1)(x-2)<0 \(\Rightarrow\)(x+1)(x+2) sẽ trái dấu
\(TH_1\Leftrightarrow\left\{{}\begin{matrix}x+1< 0\\x-2>0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x< -1\\x>2\end{matrix}\right.\\ \Leftrightarrow2>x>-1\)
\(TH_2\Leftrightarrow\left\{{}\begin{matrix}x+1>0\\x-2< 0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x>-1\\x< 2\end{matrix}\right.\\ \Leftrightarrow2< x< -1\)(vô lí)
Vậy 2>x>-1
Câu b bạn làm tương tự nhak
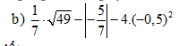Someone help me with this :')
