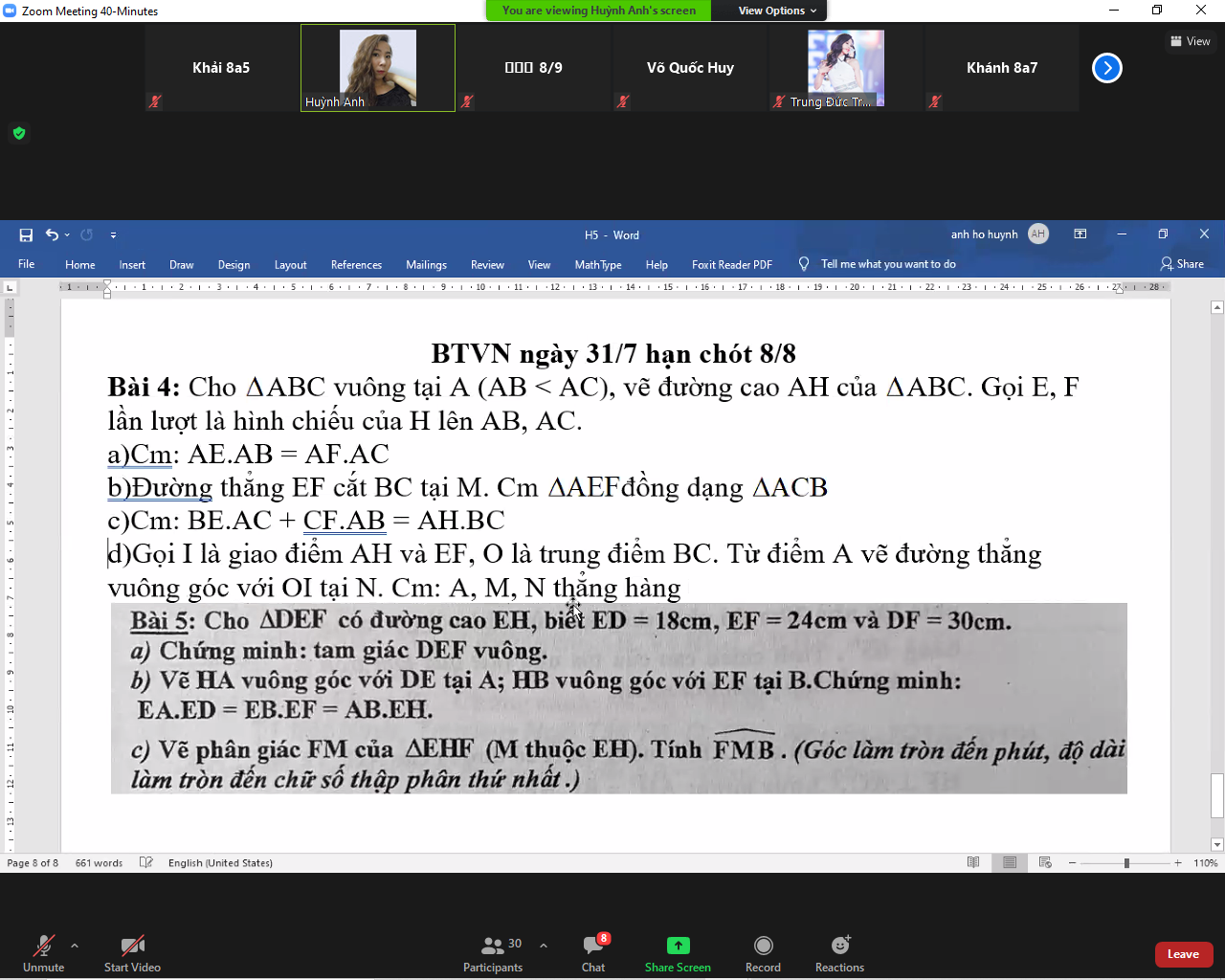
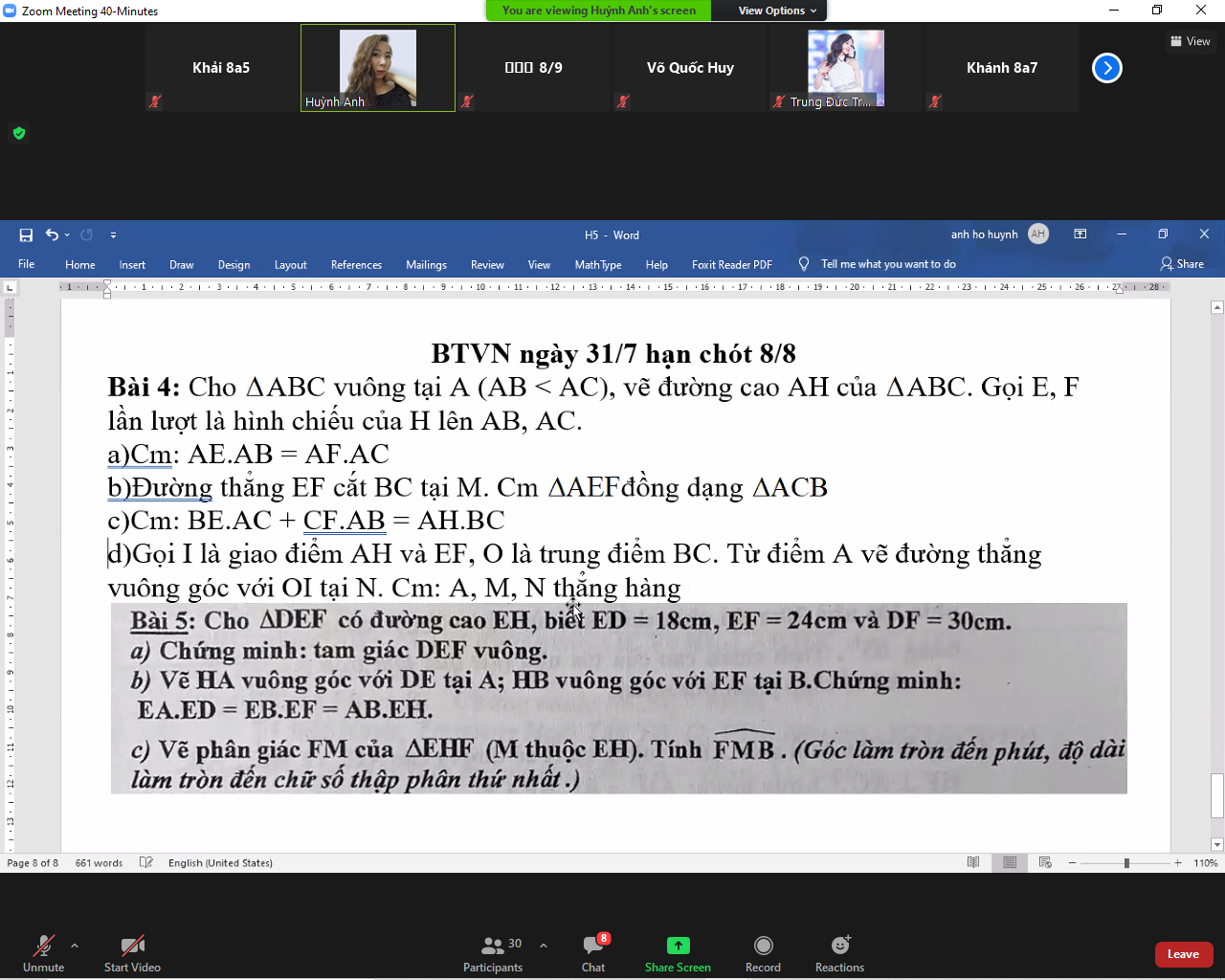
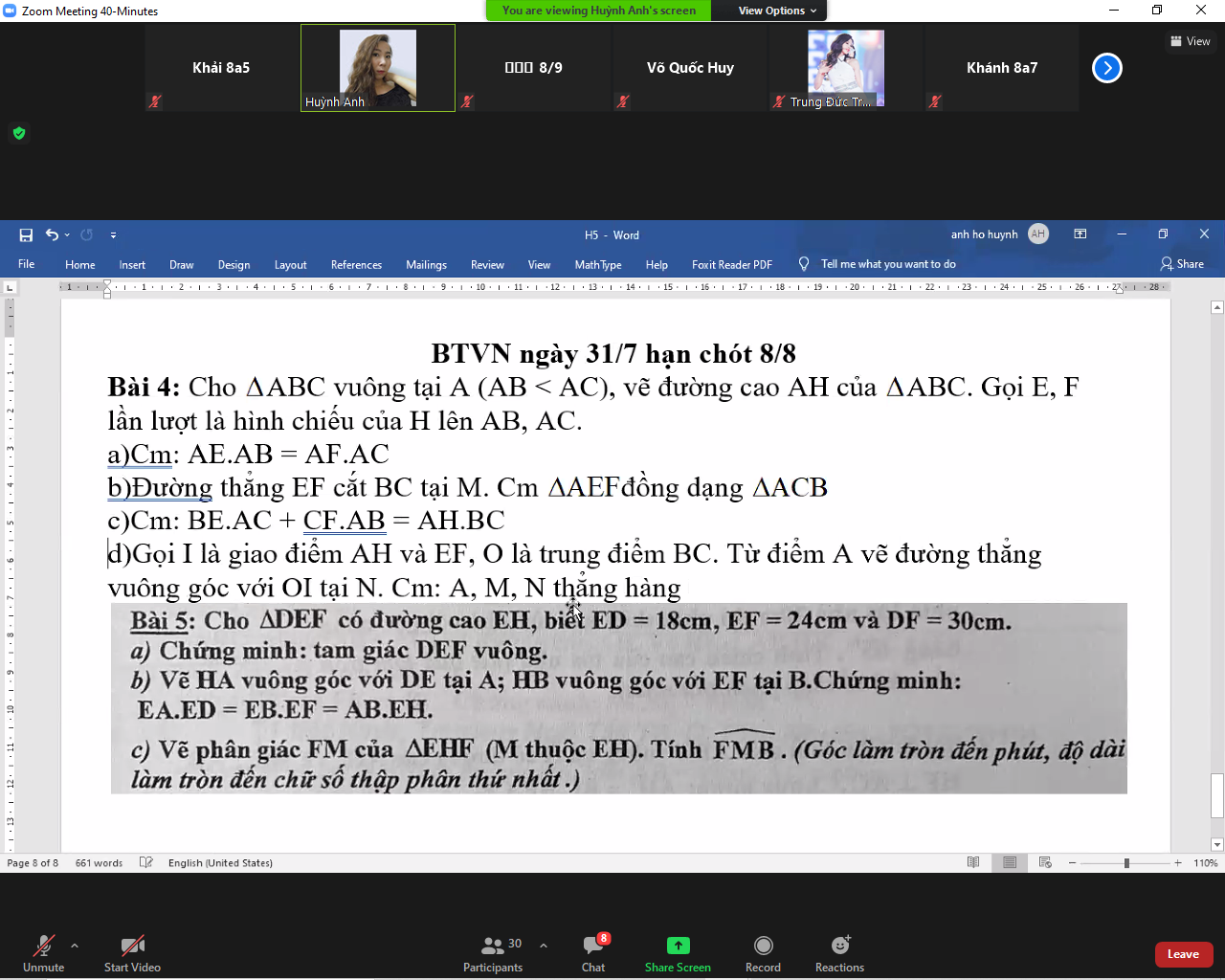
Bài 5:
a) Xét ΔDEF có \(DF^2=ED^2+EF^2\left(30^2=18^2+24^2\right)\)
nên ΔDEF vuông tại E(Định lí Pytago đảo)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔEHD vuông tại H có HA là đường cao ứng với cạnh huyền ED, ta được:
\(EA\cdot ED=EH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔEHF vuông tại H có HB là đường cao ứng với cạnh huyền EF, ta được:
\(EB\cdot EF=EH^2\)(2)
Xét tứ giác EAHB có
\(\widehat{BEA}=90^0\)
\(\widehat{EBH}=90^0\)
\(\widehat{EAH}=90^0\)
Do đó: EAHB là hình chữ nhật
Suy ra: EH=BA
hay \(EH\cdot BA=EH^2\)(3)
Từ (1), (2) và (3) suy ra \(EA\cdot ED=EB\cdot EF=EH\cdot BA\)
















 giups mik vs
giups mik vs