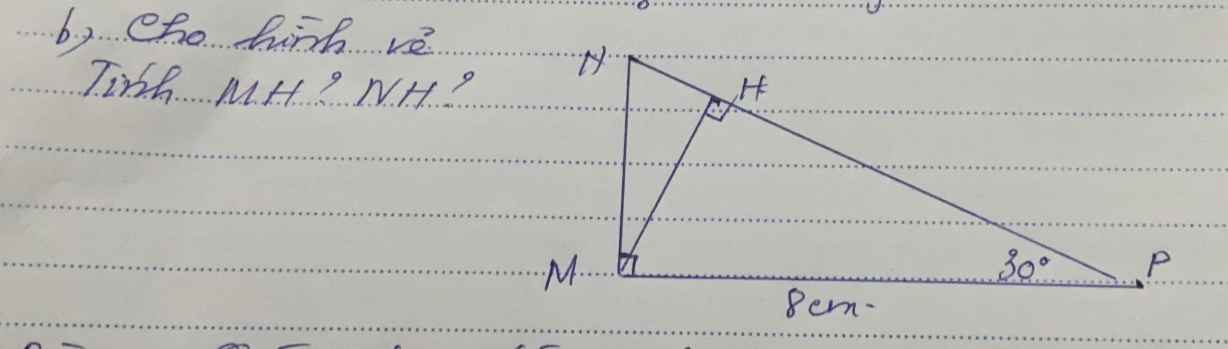
Áp dụng tỉ số lượng giác của góc nhọn vào \(\Delta MHP\), ta có:
\(\cos30\text{°}=\dfrac{MH}{8}\Rightarrow MH=8.\cos30\text{°}=4\sqrt{3}\left(cm\right)\)
Mặt khác, \(\text{∠}MNP=90\text{°}-30\text{°}=60\text{°}\)
Áp dụng tí số lượng giác của góc nhọn vào \(\Delta MHN\), ta có:
\(\tan60\text{°}=\dfrac{4\sqrt{3}}{NH}\Rightarrow NH=4\sqrt{3}.\tan60\text{°}=12\left(cm\right)\)
Lời giải:
Xét tam giác $MHP$ vuông tại $H$ thì:
$\frac{MH}{MP}=\sin P=\sin 30^0=\frac{1}{2}$
$\Rightarrow MH=\frac{MP}{2}=4$ (cm)
Theo định lý Pitago:
$HP=\sqrt{MP^2-MH^2}=\sqrt{8^2-4^2}=4\sqrt{3}$
Theo hệ thức lượng trong tam giác vuông:
$MH^2=NH.HP$
$\Leftrightarrow 4^2=4\sqrt{3}.NH$
$\Leftrightarrow NH=\frac{4\sqrt{3}}{3}$ (cm)